В наблюдаемой Вселенной доминирует вакуум; по плотности энергии он превосходит все `обычные' формы космической материи вместе взятые. Вакуум создает космическую анти-гравитацию, которая управляет динамикой космологического расширения в современную эпоху. В результате космологическое расширение ускоряется, а 4-мерное пространство-время мира становится тем временем статическим. На это определенно указывают недавние наблюдательные исследования далеких вспышек сверхновых звезд. Открытие космического вакуума влечет за собой коренной пересмотр устоявшихся представлений о современном состоянии Вселенной. Оно ставит ряд новых принципиальных проблем как в космологии, так и в фундаментальной физике. Почему плотность космического вакуума имеет именно то значение, которое найдено в наблюдениях? Почему различные компоненты космической среды имеют разные, но все же близкие по порядку величины наблюдаемые значения плотности? Вместе с тем это открытие, сделанное на больших космологических расстояниях (сотни и тысячи мегапарсек), проливает свет на динамику нашей близкой окрестности во Вселенной, на движения галактик в локальном объеме с радиусом до 10-20 Мпк, где космологическое расширение и было первоначально обнаружено.
Космология - наука наблюдательная. До недавнего времени она покоилась на двух фундаментальных наблюдательных открытиях: в 1929 г. Хаббл открыл космологическое расширение, а в 1965 г. Пензиас и Вилсон обнаружили реликтовое излучение. Между этими событиями в науке о Вселенной прошло четверть века; спустя еще примерно столько же лет в космологии произошло новое не менее значительное событие: в 1998-99 гг. две группы астрономов-наблюдателей открыли космическую анти-гравитацию и космический вакуум [1]. В работе участвовало большое число астрономов (около ста в общей сложности), одной группой руководил Адам Райес, другой - Сол Перлмуттер; исследования продолжаются и сейчас, они приобретают все больший размах, в них включаются новые и новые специалисты-наблюдатели, а за ними и теоретики.
Главный смысл новейших открытий в космологии таков. В наблюдаемой Вселенной доминирует физический вакуум; по плотности энергии он превосходит все `обычные' формы космической материи вместе взятые. Вакуум создает космическую анти-гравитацию, которая управляет динамикой космологического расширения в современную эпоху. Из-за этого космологическое расширение ускоряется, а 4-мерное пространство-время мира становится тем временем статическим.
Скажем с самого начала, что это не теории или гипотезы, которые еще предстоит проверить на опыте, а прямое следствие надежных наблюдательных данных. Открытие сделано на основании изучения далеких вспышек сверхновых звезд. Из-за их исключительной яркости, сверхновые можно наблюдать на очень больших, по-настоящему космологических расстояниях. Опуская другие детали, скажем, что использовались данные о сверхновых определенного типа (Ia), которые принято считать `стандартыми свечами'; их собственная светимость действительно лежит в довольно узких пределах (эксперты по сверхновым продолжают между тем спорить, в каких именно). Это позволяет проследить, как видимая, регистрируемая яркость источников зависит от расстояния до них. Конечно, на небольших расстояниях это классический закон обратных квадратов; но на очень большом удалении источников становятся существенными космологичесие эффекты (соответствующая базовая формула давно уже была заготовлена в `Теории поля' Л.Д. Ландау и Е.М. Лифшица [2]), и, значит, характер зависимости позволяет в принципе узнать нечто новое о всей Вселенной.
Первая группа наблюдателей [1], сообщившая о своих результатах в 1998 г., располагала данными о всего нескольких сверхновых нужного типа на нужных расстояниях; но уже и этого было достаточно, чтобы заметить космологический эффект в законе убывания видимой яркости с расстоянием; точнее, лучше смотреть не на расстояния, а на красные смещения, как это обычно и делается в случае далеких источников. Оказалось, что убывание яркости происходит заметно быстрее, в среднем, чем этого следовало бы ожидать по космологической теории, которая три года назад считалась стандартной. Такое дополнительное потускнение означает, что данному красному смещению соответствует некоторая эффективная добавка расстояния. Но это возможно тогда (и, как все сейчас думают, только тогда), когда космологическое расширение происходит с ускорением, т.е. когда скорость удаления от нас источника не убывает, а возрастает со временем.
Это открытие изменяет, в первую очередь, наше понимание современной стадии космологической эволюции, нынешнего состояния Вселенной. Прежде считалось, что вся история космологического расширения - это история его затухания после первоначального Большого Взрыва. Сейчас оказывается, что как раз в нашу эпоху динамика расширения перешла со стадии замедления к новой стадии ускорения. Вместе с тем открытие космического вакуума ставит ряд новых принципиальных проблем как в космологии, так и в фундаментальной физике. Почему плотность космического вакуума имеет именно то значение, которое найдено в наблюдениях? Почему различные компоненты космической среды имеют разные, но все же близкие по порядку величины наблюдаемые значения плотности? Вместе с тем это открытие, сделанное на больших космологических расстояниях (сотни и тысячи мегапарсек), проливает свет на динамику нашей близкой окрестности во Вселенной, на движения галактик в локальном объеме с радиусом до 10-20 Мпк, где космологическое расширение и было первоначально обнаружено.
Обо всем этом и пойдет речь ниже; текст, подготовлен специально для astronet.ru. Раннюю журнальную версию статьи см. в Успехах Физических Наук, том 171, No. 11, стр. 1153-1174, 2001.
Да, главное в космологии, как и во всякой естественно-научной дисциплине, - это конкретные факты о реальном мире. Но замечательное обстоятельство состоит в том, что все три важнейшие открытия в космологии были заранее предсказаны теорией. Космологическое расширение было предсказано Фридманом в 1922-24 гг., а существование реликтового излучения - его учеником по Петроградскому университету Гамовым. Присутствие в мире космической анти-гравитации тоже было предсказано; это было сделано в 1917 г. Эйнштейном.
Следуя давней, уходящей к истокам классической науки традиции, Эйнштейн полагал, что Вселенная как целое должна быть вечной и неизменной. Он считал, что с помощью вселенской анти-гравитации можно уравновесить гравитацию вещества во Вселенной и обеспечить неподвижность распределения вещества, а значит и статичность самой Вселенной. Для описания анти-гравитации Эйнштейн специально ввел в общую теорию относительности новую константу, которая так и называется космологической постоянной. Конечно, это была гипотеза, и притом весьма смелая. Величина же космологической постоянной не выводилась из какой-либо теории, а подлежала наблюдательному определению.
Физическая интерпретация космологической постоянной складывалась постепенно, десятилетие за десятилетием, начиная с работ де Ситтера, Леметра, Толмена, Бонди. Сейчас считается oбщепринятым, что космологическая постоянная описывает космический вакуум, т.е. такое состояние космической энергии, которое обладает постоянной во времени и всюду одинаковой в пространстве плотностью - и притом в любой системе отсчета. По этим свойствам вакуум принципиально отличается от всех других форм космической энергии, плотность которых неоднородна в пространстве, падает со временем в ходе космологического расширения и может быть разной в разных системах отсчета. Если оставить в стороне представление о статичности Вселенной, то гипотеза Эйнштейна была в действительности предположением о существовании в мире космического вакуума. И это предположение наконец подтвердилось в астрономических наблюдениях.
Хотя вакуум чаще всего называют космическим, он присутствует повсюду и фигурирует в атомной физике и микрофизике, где он представляет собой наинизшее энергетическое состояние квантовых полей. Это тот самый вакуум, в котором разыгрываются взаимодействия элементарных частиц. Физический вакуум непосредственно проявляется экспериментально, например, в лэмбовском сдвиге спектральных линий атомов и эффекте Казимира.
В таких экспериментах присутствие вакуума несомненно, но при этом значение его энергии ускользает от измерения. Последнее связано с тем принципиальным обстоятельством, что во всех - кроме гравитации! - физических взаимодействиях проявляется только разность энергий физической системы в различные моменты времени и/или в различных точках пространства, но не величина энергии в данном состоянии физической системы. Лишь гравитация "чувствует" саму энергию, а не ее разности. Грандиозным инструментом, естественной экспериментальной установкой для открытия физического вакуума послужила вся наблюдаемая Вселенная, в которой вакуум оказался доминирующим по энергии и по создаваемой ею гравитации.
В принципиальном плане проблема вакуума, его физическая природа является, как полагают, наиболее важной и вместе с тем самой сложной во всей современной фундаментальной физике [3,4].
Важные изменения в космологии, связанные с последними открытиями в в этой науке, произвели сильное впечатление на космологов и близких к космологии физиков и астрономов. По этому поводу появились также и разнообразные комментарии в популярной литературе и широкой печати. Иногда можно услышать или прочитать, что новая картина мира заставляет отказаться от привычной космологической теории Фридмана. Но это, конечно, не так. Теория, созданная Фридманом, является столь общей, столь богатой и глубокой, что в ней в действительности содержится в качестве допустимой возможности и переход космологического расширения от замедления к ускорению. Математически это обеспечивается тем, что в теории Фридмана присутствует эйнштейновская космологическая постоянная; она-то и способна создавать (вернее, представлять в решении) анти-гравитацию, которая вызывает ускорение расширения.
Как известно, в `Теории поля' [2] решение Фридмана представлено в варианте без вакуума, без космологической постоянной. В оригинальных работах Фридмана 1922-1924 гг. (они были впервые опубликованы по-немецки; русский перевод см. в Успехах Физических Наук за 1963 год [5]) эта постоянная может быть и нулевой, и отличной от нуля. Когда писалась `Теория поля', никто не сомневался, что с открытием космологического расширения все основания для введения в общую теорию относительности космологической постоянной полностью и окончательно отпали. Так считал и Эйнштейн, назвавший однажды (в разговоре с Гамовым в Принстоне) идею космологической постоянной своим самым большим промахом (biggest blunder) в науке. По словам Ландау, космология часто ошибается и никогда не сомневается.
Интерес к модели Эйнштейна, к модели де Ситтера, в которой вовсе нет вещества и имеется только вакуум, к космическому вакууму и космологической постоянной то совсем исчезал в космологии, то время от времени снова возникал по разным причинам, и на эту тему немало сказано и написано в прежние годы, в том числе и в широко известных монографиях и учебниках [6-10]; не будем повторять то, что уже не раз излагалось с большой полнотой и основательностью и к ссылкам на книги добавим только указание на пионерские работы Э.Б. Глинера [11], которые, возможно, менее известны.
Идеи, впервые высказанные в работах [11], стали основой столь популярной и до сих пор модели инфляции в очень ранней Вселенной. Но и независимо от этой конкретной модели и любых ее известных версий, идеи Глинера служат первой и пока единственной разумной гипотезой о физической причине космологического расширения: по Глинеру, расширение вещества обязано своим происхождением анти-гравитации космологического вакуума, а само вещество появилось в результате квантовых флуктуаций того же вакуума. Эти идеи высоко оценил (хотя и далеко не сразу) Я.Б. Зельдович; с самого начала отдавали им должное А.Д. Сахаров и Л.Э. Гуревич.
Инфляция - совсем особая большая и интересная тема, обсуждение которой лежит вне рамок данной статьи; о ней и без того немало сказано и написано в последние 15-20 лет. Эта красивая гипотеза позволила привлечь в космологию самые яркие идеи физики элементарных частиц и тем самым чрезвычайно обогатить современную космологическую науку. Но все же приходится признать, что при всем этом модель инфляции не смогла предсказать измеренное сейчас значение плотности вакуума. Она не дает количественных указаний на связь обнаруженной в наблюдениях плотности вакуума с начальным (исключительно высоким) значением плотности вакуума в раннюю эпоху инфляции. Как и почему первоначальная огромная плотность вакуума (или инфляционного скалярного поля) упала именно до ее современного значения - самый трудный вопрос для этой модели; а без его решения повисает в воздухе многое из того, что модель обещает объяснить.
Стоит подчекнуть, что само существование первичного инфляционного вакуума никак до сих пор не доказано в эксперментальном или наблюдательном плане, так что модель инфляции не имеет независимого эмпирического основания. В теоретическом плане ситуация тоже не слишком благоприятна; дело в том, что модель инфляции предполагает далекую экстраполяцию известных физических законов. Например, законы гравитации, проверенные экспериментально для расстояний до долей миллиметра, экстраполируются к планковским масштабам длины, которые на 30 порядков величины меньше. Похоже, что по-настоящему глубокая и основательная разработка оригинальных идей Глинера остается все еще делом будущего.
Далее в этой статье обсуждается не гипотетический первичный вакуум, а тот реальный космический вакуум, который присутствует в реальной современной Вселенной и обнаружен по наблюдениям сверхновых.
Как уже сказано, вакуум явился в космологию с эйнштейновской космологической
постоянной ![]() , и его плотность выражается через значение этой
постоянной:
, и его плотность выражается через значение этой
постоянной:
| (1) |
Вакуум обладает не только определенной плотностью энергии, но также и
давлением. Если плотность вакуума положительна, то его давление отрицательно.
Связь между давлением и плотностью, т.е. уравнение состояния, имеет для вакуума
вид ![]() . Это - и только это - уравнение состояния совместимо с
определением вакуума как формы энергии с всюду и всегда постоянной плотностью,
независимо от системы отсчета.
. Это - и только это - уравнение состояния совместимо с
определением вакуума как формы энергии с всюду и всегда постоянной плотностью,
независимо от системы отсчета.
Уравнение состояния вакуума непосредственно выводится в теории квантовых полей [12]. Но значение его плотности таким прямым путем получить в теории до сих пор не удается; как уже упомянуто выше, это острая проблема, и мы еще вернемся к этой теме в конце статьи.
Согласно фридмановской теории, тяготение создается не только плотностью
среды, но и ее давлением в комбинации ![]() . Вакуум вызывает анти-гравитацию именно потому, что его
эффективная гравитирущая энергия,
. Вакуум вызывает анти-гравитацию именно потому, что его
эффективная гравитирущая энергия, ![]() , отрицательна при положительной плотности.
, отрицательна при положительной плотности.
По наблюдательным данным о сверхновых [1], о которых
мы упоминали, плотность вакуума превышает суммарную плотность всех остальных
видов космической энергии. Значение плотностей удобно выразить в единицах
критической плотности ![]() г/см
г/см![]() , где
, где ![]() км/с/Мпк - постоянная Хаббла. Тогда относительная
плотность вакуума
км/с/Мпк - постоянная Хаббла. Тогда относительная
плотность вакуума
| (2) |
Лишь немного уступает вакууму по плотности скрытая масса, или, как чаще в
последнее время говорят, темное вещество:
| (3) |
За темным веществом следует светящееся вещество звезд и галактик; в
соотвествии с уже сказанным, его космическая плотность (средняя по всему
наблюдаемому объему мира) на порядок величины меньше плотности темного вещества:
| (4) |
Наконец, четвертой компонентой космологической среды является излучение, или
ультрарелятивистская среда, с плотностью
| (5) |
Таковы современные данные о плотностях, удовлетворяющие, как кажется, всем
имеющимся на сегодняшний день наблюдательным ограничениям. При приведенном выше
значении постоянной Хаббла эти данные совместимы как с открытой и плоской
[13,15], так, вообще говоря, и с закрытой космологическими моделями. Плоской
модели отвечает ![]() ; в открытой модели эта сумма относительных плотностей
меньше единицы, а в закрытой больше.
; в открытой модели эта сумма относительных плотностей
меньше единицы, а в закрытой больше.
Иногда в литературе, особенно научно-популярной, а тем более рекламной
(пресс-релизы, интервью и т.п.), можно встретить утверждения о том, что плоская
модель полностью доказана теоретически (со ссылкой, например, на модель
инфляции) или окончательно подтверждена такими-то и такими-то сверхточными
наблюдениями. На одном из семинаров в ГАИШ МГУ гость-докладчик сообщал в
качестве свежей новости, привезенной с последней заграничной конференции, что
плоская модель теперь уже несомненно доказана, ибо измеренная величина ![]() есть единица. Кто-то спросил из зала: А с какой точностью
измерена омега? Единица плюс-минус сколько? Так как докладчик медлил с ответом,
Р.А. Сюняев сообщил, что по его сведениям, точность была
есть единица. Кто-то спросил из зала: А с какой точностью
измерена омега? Единица плюс-минус сколько? Так как докладчик медлил с ответом,
Р.А. Сюняев сообщил, что по его сведениям, точность была ![]() в том конкретном случае...
в том конкретном случае...
Замечательно, что по поводу самих по себе цифр (2-5) в
космологическом сообществе установилось небывалое до того всеобщее единодушие и
согласие, которое - ввиду уникальности явления - получило специальное название:
космический конкорданс [15]. В одном
только пункте конкорданс не полон; одни считают, что открыт именно вакуум, тогда
как другие предпочитают иную интерпретацию, предполагая, что космологическое
ускорение создается не вакуумом, а неизвестной до сих пор и полностью
гипотетической квинтэссенцией. Под последней понимается [16] особая
форма космической энергии с уравнением состояния ![]() , где
, где ![]() - постоянный параметр, значения которого лежат в
интервале
- постоянный параметр, значения которого лежат в
интервале ![]() . Легко видеть, что эффективная гравитирующая плотность
отрицательна для этого вида энергии. Это значит, что не будучи вакуумом,
квинтэссенция тоже способна создавать анти-гравитацию, а значит и ускорение
космологического расширения. В картине мира классической древности квинтэссенция
- пятая стихия, плюс к земле, воде, воздуху и огню; это космическая субстанция,
и из квинтэссенции, как считалось, состоят небесные тела. Слово красивое,
гипотеза популярна; это и понятно, она создает новую `степень свободы' в
космологии; остается дождаться новых интересных результатов на этом пути.
. Легко видеть, что эффективная гравитирующая плотность
отрицательна для этого вида энергии. Это значит, что не будучи вакуумом,
квинтэссенция тоже способна создавать анти-гравитацию, а значит и ускорение
космологического расширения. В картине мира классической древности квинтэссенция
- пятая стихия, плюс к земле, воде, воздуху и огню; это космическая субстанция,
и из квинтэссенции, как считалось, состоят небесные тела. Слово красивое,
гипотеза популярна; это и понятно, она создает новую `степень свободы' в
космологии; остается дождаться новых интересных результатов на этом пути.
В этом месте стоит, по-видимому, сказать о космологической терминологии, которая частично изменилась после и вследствие открытия космического вакуума. Это не только появление конкорданса и квинэссенции; есть и другие новые термины, которыми тоже широко пользуются в последние 2-3 года, хотя их содержание все еще и не вполне устоялось. Различные компоненты космологической среды все чаще называют формами космической энергии, включая сюда и вакуум как одну из них. Скрытые массы, которые считаются холодными, т.е. нерелятивистскими, называют и темной энергией, и темной материей. В некоторых публикациях темной энергией называют вакуум и квинтэссенцию вместе (но это, кажется, не очень удачное нововведение). `Обычное' вещество называют барионами, хотя, конечно, в нем есть и электроны, а из барионов имеются в виду чаще всего только протоны и нейтроны. Реликтовое излучение, гравитоны и все вместе ультрарелятивистские частицы и поля космологической природы называют релятивистской энергией.
В статье Я.Б. Зельдовича [17],
опубликованной в уже упоминавшемся фридмановском выпуске Успехов Физических Наук
за 1963 г. (тогда отмечалось сороколетие теории расширяющейся Вселенной),
обьясняется, как динамику космологического расширения можно наглядно представить
на языке ньютоновской механики. Существует способ рассуждений, впервые
предложенный Е.А. Милном и У.Г. МакКри в начале 1930-х годов, который позволяет
избежать всех (точнее, почти всех) парадоксов ньютоновского тяготения, которые
возникают при попытке применить классическую механику к неограниченному,
бесконечному в пространстве распределению тяготеющей массы; при этом удается
получить результат, который в точности совпадает с тем, что дает релятивистская
теория Фридмана. Оказывается, что о бесконечности можно забыть, если рассмотреть
шар конечных размеров, мысленно выделенный из общего однородного распределения
вещества. На динамику шара внешние слои вещества не влияют, так как они
сферически-симметричны, а внутренняя масса шара действует на точку на его
поверхности так, как если бы вся эта масса была сосредоточена в центре шара.
Тогда закон обратных квадратов дает уравнение движения для частицы на
поверхности шара:
| (6) |
| (7) |
Воспользуемся этим приемом чтобы показать роль вакуума в динамике
космологического расширения. Если в полную гравитирующую плотность шара ![]() включить плотности всех четырех названных выше
компонент космической среды, то получим
включить плотности всех четырех названных выше
компонент космической среды, то получим
| (8) |
В космологической модели Эйнштейна имеется только вакуум и нерелятивистское
вещество с плотностью ![]() ; поэтому в такой модели
; поэтому в такой модели ![]() . Мир Эйнштейна статичен, так как эффективная
гравитирующая плотность
. Мир Эйнштейна статичен, так как эффективная
гравитирующая плотность ![]() считается в этой модели равной нулю. Из условия
считается в этой модели равной нулю. Из условия
![]() вытекает связь между плотностями,
вытекает связь между плотностями, ![]() , что и описывает баланс гравитации вещества и
анти-гравитации вакуума. В этом случае сила и ускорение в уравнении движения (6) для шара
равны нулю, и для неизменности его радиуса остается только потребовать, чтобы и
скорость частиц шара равнялась нулю. В модели Фридмана эти условия
необязательны; отсюда - возможность динамики и эволюции, шар может, вообще
говоря, сжиматься или расширяться.
, что и описывает баланс гравитации вещества и
анти-гравитации вакуума. В этом случае сила и ускорение в уравнении движения (6) для шара
равны нулю, и для неизменности его радиуса остается только потребовать, чтобы и
скорость частиц шара равнялась нулю. В модели Фридмана эти условия
необязательны; отсюда - возможность динамики и эволюции, шар может, вообще
говоря, сжиматься или расширяться.
При адиабатическом сжатии или расширении однородного шара связь между
изменением плотности и давлением описывается уравнением
| (9) |
| (10) |
Если подставить соотношения (8,10) в уравнение
движения (6),
то последнее можно один раз проинтегрировать по времени:
| (11) |
| (12) |
Интеграл ![]() для вещества без давления появился (и был
обозначен таким образом) в первой космологической работе Фридмана [5] - см.
формулу (8)
этой классической статьи. Будем называть интегралы (12) для
различных форм космической энергии фридмановскими интегралами.
для вещества без давления появился (и был
обозначен таким образом) в первой космологической работе Фридмана [5] - см.
формулу (8)
этой классической статьи. Будем называть интегралы (12) для
различных форм космической энергии фридмановскими интегралами.
Как всегда, первый интеграл уравнений движения есть энергия, и величина ![]() в (11) - это
полная механическая энергия частицы в расчете на единицу массы. Кинетическая
энергия стоит в левой части уравнения (12), а
потенциальная энергия (обе эти энергии тоже относятся к единичной массе) - это
взятая с противоположным знаком сумма первых четырех слагаемых в правой части
этого уравнения. Полная энергия
в (11) - это
полная механическая энергия частицы в расчете на единицу массы. Кинетическая
энергия стоит в левой части уравнения (12), а
потенциальная энергия (обе эти энергии тоже относятся к единичной массе) - это
взятая с противоположным знаком сумма первых четырех слагаемых в правой части
этого уравнения. Полная энергия ![]() может быть положительной, отрицательной или
равной нулю; соответствующие типы движения обычно называют гиперболическим,
эллиптическим и параболическим.
может быть положительной, отрицательной или
равной нулю; соответствующие типы движения обычно называют гиперболическим,
эллиптическим и параболическим.
Замечательно, что во фридмановский космологии динамика расширяющейся
Вселенной дается уравнением точно того же вида, что и ньютоновский закон
сохранения энергии (11):
| (13) |
Точное подобие релятивистского и ньютоновского уравнений не простая
случайность; это очевидное проявление в данном случае одного из основных
принципов теоретической физики, принципа соответствия, согласно которому новая
более общая теория включает в себя в качестве предельного или частного случая
старую теорию в области ее применимости. Можно считать, что ньютоновские
уравнения для однородного шара применяются при условии, что скорость расширения
шара ![]() гораздо меньше скорости света, а гравитационный
потенциал на поверхности шара гораздо меньше скорости света в квадрате. Эти
условия определенно выполняются для шара достаточно малого радиуса. Но в мире
Фридмана все расстояния, считая и малые, изменяются пропорционально масштабному
фактору
гораздо меньше скорости света, а гравитационный
потенциал на поверхности шара гораздо меньше скорости света в квадрате. Эти
условия определенно выполняются для шара достаточно малого радиуса. Но в мире
Фридмана все расстояния, считая и малые, изменяются пропорционально масштабному
фактору ![]() ; следовательно и для малого шара
; следовательно и для малого шара ![]() . Отсюда и вытекает необходимость точного подобия
уравнений для
. Отсюда и вытекает необходимость точного подобия
уравнений для ![]() и для
и для ![]() как функции времени. Далее в формулах (9)-(11) будем
подразумевать
как функции времени. Далее в формулах (9)-(11) будем
подразумевать ![]() под стоящем там
под стоящем там ![]() .
.
(Стоит заметить, что при ньютоновском описании космологического расширения без парадоксов все же не обходится. Действительно, уравнение движения (6) записано, как нужно считать, в инерциальной системе отсчета. В этой системе частица, находящаяся в центре рассматриваемого шара, покоится; с нею связано начало координат. Но в однородном мире все без исключения частицы равноправны, и значит, точно такое же уравнение движения можно записать и в системе отсчета, связанной с частицей, которая находится, например, на поверхности того же шара. Однако частица на поверхности шара движется относительно его центра отнюдь не равномерно, а согласно уравнению (6), с отличным от нуля ускорением. Поэтому обе системы отсчета не могут быть одновременно инерциальными. Этот парадокс снимается в общей теории относительности, где равноправны все свободно падающие системы отсчета, т.е. системы отсчета, которые опираются на физические тела, беспрепятственно движущиеся в поле тяжести.)
Из уравнений (11,13) можно
видеть, что динамическая роль вакуума различна на разных этапах космологического
расширения. На ранних этапах, при малых ![]() или
или ![]() (формально при
(формально при ![]() ) слагаемое в правой части обоих уравнений,
которое описывает вакуум, должно быть меньше четырех других слагаемых (
) слагаемое в правой части обоих уравнений,
которое описывает вакуум, должно быть меньше четырех других слагаемых ( ![]() ). Значит, на этих этапах расширения влияние
вакуума несущественно. В таком случае можно проинтегрировать уравнения (11,13) в
пренебрежении вакуумом (см., например, [18]) и тем
самым найти решение задачи при условии динамического доминирования обычного
вещества и излучения. Так как тяготение обычного вещества и излучения создает
отрицательное ускорение,
). Значит, на этих этапах расширения влияние
вакуума несущественно. В таком случае можно проинтегрировать уравнения (11,13) в
пренебрежении вакуумом (см., например, [18]) и тем
самым найти решение задачи при условии динамического доминирования обычного
вещества и излучения. Так как тяготение обычного вещества и излучения создает
отрицательное ускорение, ![]() , космологическое расширение происходит с
замедлением на этих ранних этапах эволюции мира.
, космологическое расширение происходит с
замедлением на этих ранних этапах эволюции мира.
При больших временах роль вакуума становится существенной, и, как следует из
уравнений (11,13), рано или
поздно наступает этап динамического преобладания вакуума, когда вакуумное
слагаемое в правой части этих уравнений оказывается много больше трех других
слагаемых справа, описывающих не-вакуумные компоненты космической среды. В этом
предельном случае больших времен (формально при ![]() ) тяготением не-вакуумных компонент можно
пренебречь, и решение уравнений (11,13) имеет вид:
) тяготением не-вакуумных компонент можно
пренебречь, и решение уравнений (11,13) имеет вид:
| (14) |
Так как вакуум с положительной плотностью создает эффективную анти-гравитацию
(его эффективная гравитирующая плотность ![]() , как мы уже не раз говорили), ускорение
, как мы уже не раз говорили), ускорение ![]() оказывается положительным, когда в динамике
расширения доминирует вакуум, и решение (14) описывает
космологическое расширение, которое ускоряется со временем. Для всех трех
вариантов модели Фридмана, отвечающих трем типам динамики, космологическое
расширение продолжается, согласно (14),
неограниченно долго. В пределе больших времен расширение происходит по
экспоненциальному закону для всех трех вариантов.
оказывается положительным, когда в динамике
расширения доминирует вакуум, и решение (14) описывает
космологическое расширение, которое ускоряется со временем. Для всех трех
вариантов модели Фридмана, отвечающих трем типам динамики, космологическое
расширение продолжается, согласно (14),
неограниченно долго. В пределе больших времен расширение происходит по
экспоненциальному закону для всех трех вариантов.
Смена замедления ускорением и переход к доминированию вакуума в динамике
космологического расширения соответствует равенству плотностей ![]() , которое имеет, очевидно, тот же смысл, что и в
статической модели Эйнштейна. Но в модели Фридмана это равенство возможно только
в один момент времени, и в этот единственный момент
, которое имеет, очевидно, тот же смысл, что и в
статической модели Эйнштейна. Но в модели Фридмана это равенство возможно только
в один момент времени, и в этот единственный момент ![]() ускорение
ускорение ![]() обращается в нуль. Соответствующее красное
смещение
обращается в нуль. Соответствующее красное
смещение
| (15) |
Как мы говорили, эффект космологического ускорения, открытый в наблюдениях
сверхновых, проявляется в зависимости их блеска от красного смещения для больших
красных смещений, - больших, но не превышающих ![]() , как и должно быть, поскольку в более ранние
времена расширение не ускорялось, а еще замедлялось.
, как и должно быть, поскольку в более ранние
времена расширение не ускорялось, а еще замедлялось.
В космологическом решении (14) хаббловская
постоянная есть ![]() , практически для любого
, практически для любого ![]() вскоре после перехода к доминированию вакуума.
На стадии полного преобладния вакуума постоянная Хаббла не зависит от времени и
определяется только значением плотности космического вакуума. Легко проверить,
что эта связь постоянной Хаббла и плотности вакуума согласуется с измеренными
значениями этих величин (в пределах ошибки измерений), - см. данные, приведенные
в п.2. Существенно, что речь здесь идет о двух независимых типах космологических
измерений.
вскоре после перехода к доминированию вакуума.
На стадии полного преобладния вакуума постоянная Хаббла не зависит от времени и
определяется только значением плотности космического вакуума. Легко проверить,
что эта связь постоянной Хаббла и плотности вакуума согласуется с измеренными
значениями этих величин (в пределах ошибки измерений), - см. данные, приведенные
в п.2. Существенно, что речь здесь идет о двух независимых типах космологических
измерений.
Остается теперь записать решение фридмановского космологического уравнения
(13) для
всех времен:
| (16) |
Интересно, что в обоих предельных случаях, при ![]() и при
и при ![]() , динамика космологического расширения не зависит
от знака полной энергии
, динамика космологического расширения не зависит
от знака полной энергии ![]() или знака пространственной кривизны
или знака пространственной кривизны ![]() , как это видно из уравнения (16). Для всех
трех вариантов динамики и кривизны расширение начинается в параболическом
режиме; затем в течение конечного времени может проявиться возможное отличие
динамики расширения от этого режима, а после этого расширение вновь выходит на
параболический режим и сохраняет этот тип движения неограниченно долго.
, как это видно из уравнения (16). Для всех
трех вариантов динамики и кривизны расширение начинается в параболическом
режиме; затем в течение конечного времени может проявиться возможное отличие
динамики расширения от этого режима, а после этого расширение вновь выходит на
параболический режим и сохраняет этот тип движения неограниченно долго.
Легко видеть, что возможные отличия от параболичности в действительности невелики при значениях плотностей (2)-(5). В соответствии с фридмановской теорией, последнее означает, что отклонения от плоской геометрии 3-пространства тоже не могут быть большими в реальном мире. Тем самым в обновленной стандартной космологии сама собой решается так наз. проблема плоскостности, которую еще недавно рассматривали как серьезную трудность этой науки.
Перейдем от динамики мира к его геометрии. Это второй важнейший аспект
современной стандартной космологической модели. Геометрия четырехмерного мира
Фридмана описывается метрическим элементом
| (17) |
Вместе с решением (16), которое
дает ![]() как функцию времени, метрический элемент (17) содержит
весь комплекс теоретических сведений о мире, которыми располагает космология.
Согласно (17),
четырехмерный мир имеет изотропное трехмерное пространство в системе отсчета
движущегося в этом пространстве вещества. Все длины в пространстве возрастают
пропорционально масштабному фактору
как функцию времени, метрический элемент (17) содержит
весь комплекс теоретических сведений о мире, которыми располагает космология.
Согласно (17),
четырехмерный мир имеет изотропное трехмерное пространство в системе отсчета
движущегося в этом пространстве вещества. Все длины в пространстве возрастают
пропорционально масштабному фактору ![]() , так что галактики, а точнее их системы, разбегаются друг от друга, и
наблюдатель заметит и измерит их движение по красному смещению в спектре
излучаемого галактиками света. Свет распространяется вдоль нулевых
геодезических, для которых интервал (17) обращается
в нуль, и из этого вытекает - в пределе не слишком больших красных смещений -
закон Хаббла, т.е. линейная зависимость скорости удаления галактик от расстояния
до них. Теория Фридмана с динамикой, даваемой уравнением (16), и
геометрией, даваемой интервалом (17), вместе с
наблюдательными сведениями о космических плотностях (2-5) и постоянной
Хаббла - это и есть стандартная космологическая модель наших дней.
, так что галактики, а точнее их системы, разбегаются друг от друга, и
наблюдатель заметит и измерит их движение по красному смещению в спектре
излучаемого галактиками света. Свет распространяется вдоль нулевых
геодезических, для которых интервал (17) обращается
в нуль, и из этого вытекает - в пределе не слишком больших красных смещений -
закон Хаббла, т.е. линейная зависимость скорости удаления галактик от расстояния
до них. Теория Фридмана с динамикой, даваемой уравнением (16), и
геометрией, даваемой интервалом (17), вместе с
наблюдательными сведениями о космических плотностях (2-5) и постоянной
Хаббла - это и есть стандартная космологическая модель наших дней.
Для нас сейчас интересны прежде всего те особенные черты новой картины мира,
которые связаны с присутствием во Вселенной космического вакуума. Если принять
для ![]() экспоненциальную временную зависимость,
соответствующую, согласно только что сказанному, динамическому доминированию
вакуума, то решение Фридмана превратится в знаменитое решение де Ситтера,
полученное в 1917 г. - еще до решений Фридмана (который, кстати, отзывался о де
Ситтере с почтением и аккуратно ссылался на его работы). Хаббл указывал на
решение де Ситтера как на возможную теоретическую модель открытого им
космологического расширения. В работах [11] оно
использовалось для описания первоначального разгона космического вещества; по
теории инфляции, эта стадия длилась не более долей секунды.
экспоненциальную временную зависимость,
соответствующую, согласно только что сказанному, динамическому доминированию
вакуума, то решение Фридмана превратится в знаменитое решение де Ситтера,
полученное в 1917 г. - еще до решений Фридмана (который, кстати, отзывался о де
Ситтере с почтением и аккуратно ссылался на его работы). Хаббл указывал на
решение де Ситтера как на возможную теоретическую модель открытого им
космологического расширения. В работах [11] оно
использовалось для описания первоначального разгона космического вещества; по
теории инфляции, эта стадия длилась не более долей секунды.
Решение де Ситтера - частный случай решения Фридмана, отвечающий формально
полному отсутствию в мире не-вакуумных форм энергии. Метрический элемент (17) при ![]() представляет это решение в системе отсчета разлетающихся
(с ускорением) пробных частиц. Пробными, т.е. негравирующими, становятся в этом
предельном случае все не-вакуумные компоненты космической среды.
представляет это решение в системе отсчета разлетающихся
(с ускорением) пробных частиц. Пробными, т.е. негравирующими, становятся в этом
предельном случае все не-вакуумные компоненты космической среды.
Самое важное свойство решения де Ситтера состоит в том, что описываемое им пространство-время статично - оно имеет не зависящие от времени 4-инварианты. Это означает, что метрика де Ситтера может быть приведена к виду, при котором никакого расширения в ней нет. И действительно, мир, заполненный вакуумной энергией с постоянной и неизменной во времени и пространстве плотностью, и сам должен быть неизменным во времени и однородным в пространстве. В таком мире все события, т.е. четырехмерные точки, неразличимы, а это означает, что в нем нигде ничего не происходит, и потому этот мир вечен, неизменен и идеально симметричен по своим геометрическим свойствам.
При таких условиях должна существовать система отсчета, в которой метрический
элемент решения де Ситтера не содержит зависимости от времени. Приведем для
конкретности одну из возможных статических форм решения де Ситтера:
| (18) |
Существуют и другие формы этого решения, в которых трехмерное пространство
выглядит иначе. Но во всех случаях вакуум, заполняющий любое из этих
пространств, имеет всюду однородную и всегда постоянную плотность ![]() . Численное значение плотности вакуума во всех этих случаях одно и то
же, так что измерив это значение в системе отсчета, сопутствующей расширяющемуся
веществу, как это реально и сделано с помощью наблюдений сверхновых, мы знаем,
что оно в точности такое и при любых других способах измерений в какой угодно
системе отсчета.
. Численное значение плотности вакуума во всех этих случаях одно и то
же, так что измерив это значение в системе отсчета, сопутствующей расширяющемуся
веществу, как это реально и сделано с помощью наблюдений сверхновых, мы знаем,
что оно в точности такое и при любых других способах измерений в какой угодно
системе отсчета.
Важно, что в любой из возможных форм записи интервала де Ситтера даваемая ими
дифференциальная геометрия четырехмерного мира в точности та же, что и в форме
(18). Это
геометрия четырехмерного пространства-времени постоянной кривизны. Четырехмерная
кривизна мира ![]() прямо связана с фридмановским интегралом для вакуума:
прямо связана с фридмановским интегралом для вакуума: ![]() . Эта кривизна (риманова) положительна при положительном значении
плотности вакуума.
. Эта кривизна (риманова) положительна при положительном значении
плотности вакуума.
Двумерным пространством постоянной положительной кривизны является, как известно, сфера. Трехмерное пространство постоянной положительной кривизны, которое фигурирует в модели Эйнштейна и в одной из трех (закрытой) моделях Фридмана, назывется гиперсферой. Четырехмерное пространство-время постоянной положительной кривизны - это тоже некая `сфера', хотя и сильно отличающаяся (прежде всего, по сигнатуре метрики) от своих двумерного и трехмерного аналогов.
Четырехмерная кривизна ![]() обращается в нуль, если только плотность вакуума положить равной нулю;
при этом метрика (18) переходит в
галилееву (или, что то же, лоренцову) метрику специальной теории
относительности. Формально говоря, в мире с нулевой четырехмерной кривизной нет
ничего, даже выкуума. По существу же это означает, что специальная теория
относительности - применительно к космологическим задачам - неверна в
пространственно-временных масштабах, которые близки к фридмановскому интегралу
обращается в нуль, если только плотность вакуума положить равной нулю;
при этом метрика (18) переходит в
галилееву (или, что то же, лоренцову) метрику специальной теории
относительности. Формально говоря, в мире с нулевой четырехмерной кривизной нет
ничего, даже выкуума. По существу же это означает, что специальная теория
относительности - применительно к космологическим задачам - неверна в
пространственно-временных масштабах, которые близки к фридмановскому интегралу
![]() или превышают его.
или превышают его.
Ненулевая кривизна реального четырехмерного мира, ![]() см
см![]() , представляет собой едва ли не самую основную константу природы. Во
всяком случае это главная константа в космологии - наряду, конечно, с плотностью
вакуума, с которой она прямо связана. Фридмановский же интеграл
, представляет собой едва ли не самую основную константу природы. Во
всяком случае это главная константа в космологии - наряду, конечно, с плотностью
вакуума, с которой она прямо связана. Фридмановский же интеграл ![]() см - основная космологическая длина. Отвечающее этой длине время -
см - основная космологическая длина. Отвечающее этой длине время -
![]() млрд лет. А соответствующая масса
млрд лет. А соответствующая масса ![]() г. Из этих характерных величин длины, времени и массы
можно составить `космическую' систему единиц. Как видно из цифр, приведенных в
конце предыдущего параграфа, в современную эпоху
г. Из этих характерных величин длины, времени и массы
можно составить `космическую' систему единиц. Как видно из цифр, приведенных в
конце предыдущего параграфа, в современную эпоху ![]() , если эти величины записать в `космических' единицах.
, если эти величины записать в `космических' единицах.
Вернемся к эволюционной истории мира. Из сказанного становится ясным, что переход в расширяющейся Вселенной от стадии преобладания обычного вещества к стадии преобладания вакуума означает постепенное исчезновение динамики в четырехмерном пространстве-времени. Пространственно-временой каркас мира, можно сказать, застывает, он перестает изменяться со временем и оказывается в результате зафиксированным навечно. Но в погруженном в этот вечный и неизменный мир веществе многое еще происходит и будет происходить (например, вспыхивают сверхновые, по которым мы узнаем об ускоряющемся расширении). Однако на метрику четырехмерного мира эти процессы, события, превращения в веществе практически никак не влияют сейчас и еще меньше будут влиять в будущем. Можно сказать, что чем сильнее разгоняется космологическое расширение под воздействием антигравитирующего векуума, тем ближе наш четырехмерный мир к абсолютной статике, неизменности и полному покою. Таков самый важный динамический и геометрический эффект вакуума в космологии.
Очевидно, что в этих новых обстоятельствах традиционный вопрос о том, является ли реальная космологическая модель открытой, закрытой или плоской, теряет свою прежнюю остроту и принципиальность. А сколько было горячих споров по этому поводу, сколько дорогостоящих наблюдательных, в том числе и космических программ было нацелено на точное определение космологических параметров и тем самым на решение самой грандиозной, как считалось, проблемы естествознания. Теперь ясно, что от выбора между тремя возможными моделями трехмерной геометрии не зависит ответ на вопрос о судьбе мира, т.е. будет ли мир расширяться вечно или его наблюдаемое расширение сменится в будущем сжатием. По решению (16), космологическое расширение происходит неограниченно долго во всех трех моделях. Эти модели различаются между собой лишь тем, что их трехмерные пространства выделены тремя разными способами из одного и того же единого четырехмерного пространства-времени. По способу выделения, эти трехмерные объемы могут иметь нулевую или ненулевую кривизну. Конечно, интересно знать, какой именно знак имеет кривизна `нашего' конкретного изотропного трехмерного пространства, в котором наблюдаемое космологическое расширение происходит однородно и изотропно. Гораздо важнее, однако, то замечательное обстоятельство, что даже и независимо от этого стала известна четырехмерная геометрия пространства-времени. И об этой геометрии известно все, именно все(!), что только вообще можно узнать из общей теории относительности: это статическое пространство-время постоянной положительной кривизны, причем численное значение кривизны довольно точно измерено.
Но чего нельзя ожидать от общей теории относительности, это описания топологии четырехмерного мира, его геометрического строения как целого. В заочной полемике с Эйнштейном, Фридман обращал внимание на то, что общая теория относительности строится на дифференциальной геометрии (Фридман читал курс дифференциальной геометрии в Петроградском университете), и топологии в ней нет. Дифференциальная геометрия дает для топологии лишь некоторые ограничения общего характера, но не определяет ее. Эйнштейн же полагал, что найденное им статическое космологическое решение с положительной кривизной 3-пространства описывает Вселенную, 3-пространство которой в целом является закрытым, замкнутым в себе, подобно сфере. Но по существу это было произвольной дополнительной гипотезой, никак не вытекающей из общей теории относительности как таковой. Фридмановские модели, открытая и закрытая, называются так только в силу традиции; эти названия не должны вводить в заблуждение отосительно возможной топологии трехмерных пространств в этих моделях, - о ней реально ничего не известно.
Последнее в полной мере касается, конечно, и мира де Ситтера; известна его четырехмерная дифференциальная геометрия - она полностью описывается интервалом (18), но его топология, его геометрия в целом остается полностью открытой проблемой. Имеется множество интересных и разнообразных математически допустимых вариантов глобального строения такого мира (см. о некоторых из них в лекциях [8]). Но удастся ли когда-нибудь проверить эти варианты в наблюдениях и выбрать один из них? Как бы то ни было, топология мира становится теперь самым принципиальным, если не единственным по-настоящему важным вопросом геометрического характера в космологии современной Вселенной.
В другом (не о топологии) споре между Эйнштейном и Фридманом, споре о том, является ли мир статичным или эволюционирующим (см. об этом споре в [19,20]), оба классика оказываются в итоге правы, но каждый по-своему. Идея Эйнштейна о неизменной и вечной Вселенной реализуется хотя и не в его статической модели, но зато в идеально симметричном решении де Ситтера. А идея нестационарной Вселенной Фридмана - в его общей теории эволюции Вселенной и в наблюдаемом феномене хаббловского разбегания галактик. Идея Фридмана включает в себя, в частности, и идею Эйнштейна - в качестве предельного случая.
Когда в 1917 г. Эйнштейн опубликовал свою модель статической Вселенной, космологическое расширение было уже фактически открыто американским астрономом Весто Слайфером, который сообщил об этом в статье, вышедшей в том же знаменательном для космологии 1917-м. Правда, сообщая о разбегании космических туманностей, Слайфер не знал еще по сути и сам, что именно он открыл: ни расстояния до туманностей, ни их истинная природа тогда еще не были известны; естественно, что в его работе не было ни слова о космологии. Но и сама эта наука в ее нынешнем понимании не существовала еще до общей теории относительности (1916 г.) и первой космологической работы Эйнштейна 1917 года. Семью годами позже, в 1924 г., Фридман обсуждал открытие Слайфера на одном из своих семинаров в Петроградском университете и, по свидетельству участника семинара Д.Д. Иваненко, рассматривал это открытие в космологическом контексте, считая его - совершенно справедливо - прямым наблюдательным свидетельством в пользу теории расширяющейся Вселенной. Об открытии Слайфера сообщал и издававшийся в те годы в СССР научно-популярный журнал `Мироведение'.
Теория Фридмана предполагает, что Вселенная однородна по распределению
вещества в ней, и это действительно так. Крупномасштабное распределение галактик
статистически однородно в масштабах 100-300 Мпк и более, а изотропия Вселенной
точнее всего подтверждается реликтовым излучением, которое изотропно с точностью
по крайней мере до сотых долей процента. Фридмановская теория предсказывает, что
космологическое расширение в однородном и изотропном мире должно происходить по
линейному закону: в каждый данный момент истории мира скорость удаления обьекта,
находящегося на расстоянии ![]() от нас, пропорциональна этому расстоянию:
от нас, пропорциональна этому расстоянию: ![]() , где
, где ![]() - постоянный коэффициент, который не зависит ни от расстояния до
обьекта, ни от направления на него на небе. Эта зависимость есть прямое
следствие однородности и изотропии Вселенной; таким увидит космологическое
расширение любой наблюдатель, где бы во Вселенной он ни находился. Этот закон
был открыт Хабблом в его наблюдениях 1927-1929 гг., и постоянная
- постоянный коэффициент, который не зависит ни от расстояния до
обьекта, ни от направления на него на небе. Эта зависимость есть прямое
следствие однородности и изотропии Вселенной; таким увидит космологическое
расширение любой наблюдатель, где бы во Вселенной он ни находился. Этот закон
был открыт Хабблом в его наблюдениях 1927-1929 гг., и постоянная ![]() по справедливости носит с тех пор его имя.
по справедливости носит с тех пор его имя.
Хаббл уже знал - из своих собственных исследований, - что Вселенная это мир
галактик. Он построил диаграмму зависимости ![]() от
от ![]() для двух дюжин галактик, лучевые скорости которых он измерил, а
расстояния оценил. Оригинальная хаббловская диаграмма воспроизводится на нашем
Рис.2.
для двух дюжин галактик, лучевые скорости которых он измерил, а
расстояния оценил. Оригинальная хаббловская диаграмма воспроизводится на нашем
Рис.2.
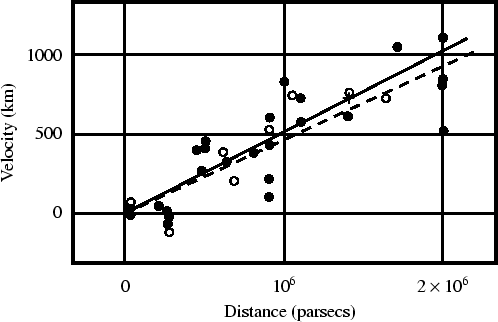 |
| Рис. 2. Оригинальная хаббловская диаграмма 1929 г. На вертикальной оси скорость должна быть в единицах км/с, а не в км. Гелиоцентрическая система отсчета. |
Измеренные Хабблом скорости были лишь немногим больше тысячи км/сек. Если
воспользоваться принятым сейчас значением постоянной Хаббла, ![]() км/сек/Мпк, то легко увидеть, что предел расстояний в его
наблюдениях составлял примерно 20 Мпк. Сам Хаббл думал тогда, что 2 Мпк; такой
была у него систематическая ошибка оценки расстояний, почти что ровно в десять
раз.
км/сек/Мпк, то легко увидеть, что предел расстояний в его
наблюдениях составлял примерно 20 Мпк. Сам Хаббл думал тогда, что 2 Мпк; такой
была у него систематическая ошибка оценки расстояний, почти что ровно в десять
раз.
Но в пределах 20 Мпк никакой однородности и изотропии во Вселенной нет; как мы только что сказали, эти свойства Вселенная приобретает лишь в масштабах 100-300 Мпк и более. На эту тему имеются обширная литература; сошлемся на книги [6-10] и свежие публикации по теме [21-30]. Распределение же вещества в ближнем объеме, напротив, крайне неравномерно: имеются группы галактик с размерами в 1 Мпк и больше, все они входят в большое скопление галактик Вирго (т.е. Дева), центр которого лежит в направлении на одноименное созвездие и находится от нас на расстоянии прибизительно в те же 20 Мпк, и т.п. Как при таких условиях здесь возможен регулярный космологический поток расширения с линейной зависимостью скорости от расстояния?
Наименьшие скорости удаления у Хаббла составляют всего одну-две сотни км/сек; и это означает, что хаббловский поток берет начало очень близко от нас, на расстояниях всего в несколько Мпк. Но это катастрофически не тот, не космологический пространственный массштаб.
Остается лишь спросить: а имеет ли открытие Хаббла какое-либо отношение к космологии?
Через 70 лет после после первой космологической публикации Хаббла, в 1999 г.,
вопрос о природе локального (до 20 Мпк) хаббловского потока был вновь отчетливо
поставлен в работе А. Сэндиджа [31] (см. также
его публикации 1972 и 1986 гг. [32,33]). К
настоящему времени наблюдениям стали доступны галактики со скоростями разбегания
в сотни тысяч км/сек, что соответствует расстояниям в тысячи Мпк. Это бесспорно
космологические масштабы. На таких масштабах линейный закон расширения надежно и
уверенно установлен, - в полном соответствии с теоретическими ожиданиями в духе
изотропных фридмановских моделей. Но что поразительней всего, для этих
глобальных космологических масштабов постоянная Хаббла имеет практически то же
самое численное значение, что и в локальном объеме до расстояний всего в 10-20
Мпк. Согласно Сэндиджу [31],
космологическое расширение прослеживается вплоть до 1.5 - 2 Мпк от нас, и
`локальный темп подобен глобальному, если только он не совпадет с ним точно, на
уровне ![]() 10 %'. Иными словами говоря, общая картина расширения выглядит так,
как если бы глобальный космологический поток и в самом деле начинался прямо
вблизи нас и, простираясь далее чуть не до горизонта мира, сохранял всюду свою
кинематическую идентичность! Но ведь это же абсолютно невозможно...
10 %'. Иными словами говоря, общая картина расширения выглядит так,
как если бы глобальный космологический поток и в самом деле начинался прямо
вблизи нас и, простираясь далее чуть не до горизонта мира, сохранял всюду свою
кинематическую идентичность! Но ведь это же абсолютно невозможно...
Такова загадка, оставленная нам Хабблом. Сэндидж, один из самых крупных космологов-наблюдателей наших дней, прямо пишет в работе 1999 г.: `мы так и остаемся с этой тайной' [31].
Приведем самые свежие наблюдательные данные о движениях галактик в местном объеме, которыми располагает группа И.Д. Караченцева в САО РАН. Основной результат таков: на гораздо большем наблюдательном материале, чем тот, который был в распоряжении Хаббла в 1929 г., и с гораздо более высокой степенью точности подтверждено и продемонстрировано существование регулярного потока расширения с линейным законом скорости для расстояний от 2 до 8 Мпк.
Группа Караченцева [34]
представила недавно два варианта хаббловской диаграммы (Рис.3, 4). Первый из
них (Рис.3)
включает в себя данные о движениях 145 галактик до расстояний 8 Мпк (по большей
части это оригинальные результаты наблюдений). Скорости измерены с точностью не
хуже 5 км/сек, точность расстояний 20 %. Скорости даны в системе отсчета центра
масс Местной Группы. Эта группа включает в себя нашу Галактику и сравнимую с ней
по массе гигантскую галактику Андромеда, находящуюся от нас на расстоянии 700
кпк; эти две галактики составляют основную массу группы. В группе имеется еще
2-3 десятка менее массивных галактик, среди которых большинство составляют
совсем небольшие галактики-карлики. Общий размер Местной Группы приблизительно 1
Мпк. Подавляющее большинство других галактик, находящихся вне Местной группы на
расстояниях до 8 Мпк (а их там не меньше двух сотен), это тоже карлики.
Измеренная по данным о 145 галактиках постоянная Хаббла составляет ![]() км/сек/Мпк, что практически совпадает с `глобальным'
значением этой величины, измеренным на масштабах в тысячи Мпк.
км/сек/Мпк, что практически совпадает с `глобальным'
значением этой величины, измеренным на масштабах в тысячи Мпк.
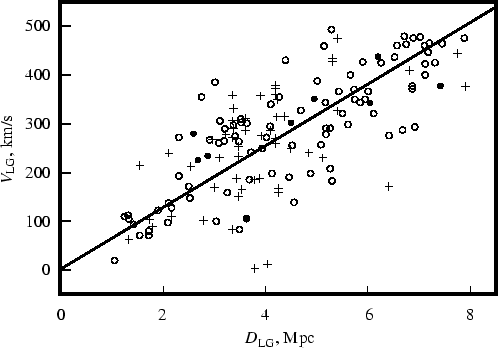 |
| Рис. 3. Хаббловская диаграмма для 145 галактик Местного объема [34]. Система центра масс Местной группы. |
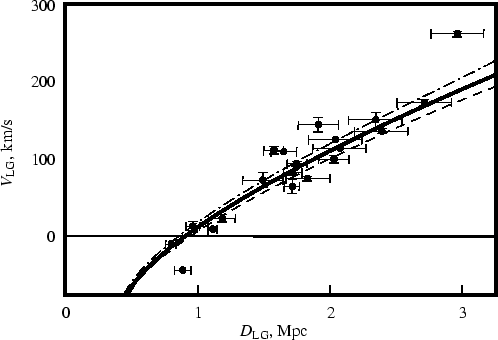 |
| Рис. 4. Хаббловская диаграмма для 20 галактик Местного объема с высокоточными расстояниями [34]. Система центра масс Местной группы. |
Дисперсия скоростей 145 галактик составляет 74 км/сек; часть этой величины обусловлена ошибками наблюдений, часть движениями галактик в составе их групп; но она может также отражать реальную анизотропию разбегания всей совокупности галактик в данном объеме. С точки зрения той проблемы, которую мы здесь обсуждаем, показательно, что величина дисперсии сравнима с регулярной линейной скоростью расширения до расстояний около 2 Мпк и заметно меньше регулярной скорости для расстояний от 3 до 8 Мпк. Средняя амплитуда отклонений от линейной регулярности, вычисленная для всего этого объема, не превышает 10 %.
Особенно интересна для наших целей диаграмма (Рис.4) для 20 галактик с высокоточными, не хуже 7 %, определениями расстояний [34]. Это галактики-карлики, находящиеся от нас на расстояниях не дальше 3 Мпк и, за редким исключением, не входящие в группы; их кинематика отражает в наиболее чистом виде динамическую обстановку в нашем ближайшем окружении. Не искаженные участием во внутригрупповых движениях, скорости этих галактик обнаруживают поразительно малый разброс вокруг линейного закона - всего 25 км/сек. Это первая надежная оценка хаотических движений галактик местного объема, которая заведомо превышает ошибки наблюдений (около 15 км/сек). И как мы видим, поток этих галактик еще спокойнее и холоднее, чем и так уже далеко не бурный общий поток во всем объеме до 8 Мпк. С точки зрения динамики, эти галактики служат в качестве очень хорошего измерительного инструмента для анализа поля скоростей, а значит и поля тяготения в местном объеме.
Высокая степень регулярности движений этих ближних галактик резко контрастирует с крайней степенью нерегулярности, сильной неоднородностью их пространственного распределеня. По данным группы Теерикорпи и Патуреля [24,35], особенно сильные нерегулярности и неоднородности наблюдаются как раз в пределах 2 - 3 Мпк, а дальше они постепенно сглаживаются (в среднем по возрастающим объемам), оставаясь, однако, и там далеко не слабыми, вплоть до расстояний в 200 Мпк.
Из всей этой наблюдаемой картины напрашивается один вывод: кинематика галактик в местном объеме имеет мало общего с их пространственным распределением. Кинематика исключительно регулярна, тогда как пространственное распределение сильно неоднородно как в этом объеме, так даже и в более обширных объемах вокруг нас. За наблюдаемой кинематикой галактик стоит динамика, которая, следовательно, с распределением масс галактик фактически не связана.
Но если не массы самих галактик, то что же тогда управляет движением этих тел в местном объеме? Такова новая физическая постановка вопроса о природе локального хаббловского потока.
В духе новейших открытий в космологии можно предположить, что хаббловским потоком управляет космологический вакуум. Такой ответ [36,37] предполагает трактовку космологического ускорения в духе космологической постоянной, т.е. вакуума (об альтернативной интерпретации в духе гипотетической квитэссенции упомянуто выше и мы еще скажем о ней далее).
Согласно наблюдениям, в окружающем нас объеме с расстояниями до 3-5 Мпк
подавляющая доля всей не-вакуумной материи концентрируется к Местной группе.
Масса Местной группы это фактически суммарная масса барионов нашей Галактики и
Андромеды плюс превышающая последнюю раз в 10 темная материя, которая заполняет
протяженные массивные гало этих двух галактик. Полная не-вакуумная масса Местной
группы ![]() солнечных масс [7,34], и она
сосредоточена в объеме с размером приблизительно в 1 Мпк.
солнечных масс [7,34], и она
сосредоточена в объеме с размером приблизительно в 1 Мпк.
Для оценки динамической картины в масштабах от 1 до 8-10 Мпк сравним две
величины: силу отталкивания, создаваемую вакуумом на некотором расстоянии ![]() от центра масс Местной группы, и силу притяжения,
создаваемую на том же расстоянии суммарной массой Местной группы. Сила
отталкивания такова:
от центра масс Местной группы, и силу притяжения,
создаваемую на том же расстоянии суммарной массой Местной группы. Сила
отталкивания такова:
| (19) |
Для грубой оценки силы притяжения, создаваемой массой Местной группы,
пренебрежем несферичностью распределения полной массы; в действительности это,
конечно, не сфера а скорее гантель, но разница в оценке все равно невелика, как
легко проверить, для тех расстояний, которые получатся в ответе. Не станем также
добавлять к массе Местной группы массы других галактик в объеме с радиусом ![]() , - это тоже не сильно изменило бы результат. Тогда в этом
первом и главном приближении
, - это тоже не сильно изменило бы результат. Тогда в этом
первом и главном приближении
| (20) |
Наша оценка, конечно, грубовата, но зато очевидна, надежна и устойчива по сути. Нетрудно сделать и более рафинированный расчет; можно построить, например, семейство поверхностей одинакового ускорения в местном объеме и найти ту из них, на которой радиальная компонента ускорения обращается в нуль. Эта поверхность в действительности не сильно отличается от сферы радиуса 2-3 Мпк. А поверхности еще большего размера и вообще практически перестают отличаться от сфер, так что для расстояний в 4-5 Мпк и более имеет место почти строго (с точностью не хуже 20-30 %) сферически-симметричное ускорение. И на этих расстояниях полностью доминирует вакуум.
В регулярном сферически-симметричном поле ускорений на расстояниях 3-4 Мпк и более естественно ожидать и регулярного движения пробных тел, каковыми являются маломассивные галактики на Рис.4, да и вообще все галактики местного объема. Но именно так реально и выглядит локальный поток в наблюдениях: он действительно весьма регулярен начиная с расстояний всего в 1.5-2 Мпк, - это так и по данным Сэндиджа [31], и на трех показанных здесь вариантах хаббловской диаграммы. Здесь нет никакого парадокса, раз в динамике местного объема доминирует вакуум с его идеально однородной плотностью. Таким образом, снимается противоречие между регулярной кинематикой галактик местного объема и крайне нерегулярным распределением не-вакуумных форм энергии в этом объеме. Начиная с расстояний в несколько Мпк, галактики хаббловского потока движутся как пробные частицы на идеально регулярном фоне вакуума, который их разгоняет (верней, подгоняет).
С открытием вакуума Вселенная в целом оказывается более однородной, чем об этом можно было судить ранее только по распределению галактик в ней. Она однородна не только в собственно космологических масштабах 100-300 Мпк и более. В динамическом смысле она однородна вокруг нас уже с расстояний в несколько Мпк. Можно сказать, что космология начинается теперь не с сотен Мпк, а с нескольких Мпк от нас. Она подступает почти вплотную к нам, к Млечному пути. И все это из-за динамического доминирования вакуума как по Вселенной в целом, так и в самых малых ее объемах вроде местного объема. (Заметим в скобках, что в местах с большей концентрацией не-вакуумной энергии вакуум доминирует с больших масштабов, чем в местном объеме; например, в богатых скоплениях галактик, таких как скопление в Коме или Вирго, радиус нулевого ускорения может составлять 10-30 Мпк.)
Критический пункт этих рассуждений - кинематическая идентичность хаббловского
потока на всем интервале масштабов от нескольких Мпк до самых больших расстояний
в мире галактик. Этот вопрос, который до сих пор ставил в тупик думающих
астрономов-наблюдателей, теперь, кажется, проясняется. Действительно, раз во
всех этих масштабах доминирует вакуум с его всюду одинаковой плотностью, то и
темп расширения, характеризуемый постоянной Хаббла, должен быть везде одинаков,
поскольку постоянная Хаббла определяется только плотностью вакуума. Согласно
решению (14), которое
справедливо всюду, где доминирует вакуум, а также и уравнению (19) на
расстояниях ![]() Mпк, постоянная Хаббла в этих условиях
Mпк, постоянная Хаббла в этих условиях ![]() .
.
В этом и состоит, как как можно полагать [36,37], разгадка той `тайны', которая существовала со времен работы Хаббла 1929 г. и о которой совсем недавно говорил Сэндидж. Мы видим, только с открытием космического вакуума стали по-настоящему ясны космологическое значение и реальный физический смысл открытия, сделанного Хабблом по наблюдениям в местном объеме Вселенной. Глубоко внутри ячейки однородности общего распределения галактик Хаббл открыл глобальный космологический феномен расширения Вселенной. Но по существу он тем самым открыл еще и космологический вакуум. А ссылка, которую он дает в своей работе на модель де Ситтера, исключительно точно попадает в цель.
Как можно было видеть выше, фридмановские интегралы - это базовые константы космологии. Для нерелятивистского вещества и излучения интегралы выражают сохранение полного числа частиц каждого данного сорта в сопутствущем объеме. Интересно, что соответствующий интеграл сопоставляется и вакууму, причем этот интеграл, как уже сказано, тоже вычисляется по общей формуле (12), хотя, конечно, интерпретация на языке частиц для вакуума не годится. По смыслу фридмановских уравнений, общее и главное в интегралах то, что они вытекают из условия адиабатичности, т.е. в данном случае из отсутствия перетока внутренней энергии из одной ее формы в другую. Такому условию удовлетворяют все четыре формы энергии, включая вакуум, после окончания процессов, связанных с трансформациями вакуума (фазовыми переходами) в очень ранней дофридмановской Вселенной (см. об этих последних процессах в книгах [6-10]).
Будучи произвольными константами интегрирования, фридмановские интегралы не ограничены никакими априорными соотношениями, кроме тривиальных, и полностью независимы друг от друга. Например, в холодной Вселенной (не правдоподобный, но формально не исключаемый заранее вариант) интеграл для излучения был бы равен нулю, тогда как интеграл для нерелятивистских частиц оставался бы отличным он нуля. Для динамики, описываемой фридмановским решением (16), интегралы служат `начальными условиями'; с точки зрения физики, они и определяются в действительности реальными физичесими условиями в ранней Вселенной на стадии генерации наблюдаемых форм космической энергии.
Вскоре после открытия реликтового излучения было замечено [50], что
фридмановские интегралы, вычисленные по известным значениям плотностей вещества
и излучения, оказываются довольно близкими друг другу по порядку величины. В
духе идей Гамова о космических совпадениях [51], было
высказано предположение [50], что
совпадение интегралов можно считать фактом более фундаментальным, чем сама
близость плотностей двух космических энергий. Действительно, найденное в [50]
соотношение ![]() см содержит в компактном виде целый комплекс разнообразных физических
связей в космологии. Нетрудно убедиться, что этих двух равенств достаточно,
чтобы дать количественную формулировку зарядовой асимметрии Вселенной,
космологической энтропия в расчете на один барион, выхода гелия в первичном
нуклеосинтезе, длительности эпохи преобладания излучения, и т.д.
см содержит в компактном виде целый комплекс разнообразных физических
связей в космологии. Нетрудно убедиться, что этих двух равенств достаточно,
чтобы дать количественную формулировку зарядовой асимметрии Вселенной,
космологической энтропия в расчете на один барион, выхода гелия в первичном
нуклеосинтезе, длительности эпохи преобладания излучения, и т.д.
Как мы сейчас увидим, два других фридмановских интеграла - для вакуума и
темной энергии - тоже близки друг к другу и к двум упомянутым интегралам. С
помощью наблюдательных данных (2-5) фридмановские
интегралы для темной энергии, барионов и ультра-релятивистских частиц могут быть
найдены, если воспользоваться еще значением современного радиуса кривизны ![]() (или нормированного масштабного фактора), - это
приближенное выражение было дано выше в п.3. Таким путем находим:
(или нормированного масштабного фактора), - это
приближенное выражение было дано выше в п.3. Таким путем находим:
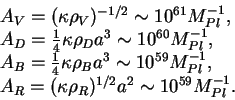 |
(21) |
Как видим, все четыре числа близки друг к другу по порядку величины [52], и
результат можно представить в компактной форме:
| (22) |
Из-за того, что ![]() как для темной энергии, так и для барионов, приближенное равенство
сответствующих двух интегралов возникает просто вследствие близости наблюдаемых
плотностей этих двух форм энергии. Однако по структуре формулы (12), для
близости значения этих интегралов к значению интеграла для вакуума требуется не
только близость всех трех плотностей, но и близость текущего радиуса кривизны
трехмерного пространства к интегралу для вакуума; это специфика эпохи
наблюдения. То же относится и к приближенному равенству интегралов для излучения
и вакуума.
как для темной энергии, так и для барионов, приближенное равенство
сответствующих двух интегралов возникает просто вследствие близости наблюдаемых
плотностей этих двух форм энергии. Однако по структуре формулы (12), для
близости значения этих интегралов к значению интеграла для вакуума требуется не
только близость всех трех плотностей, но и близость текущего радиуса кривизны
трехмерного пространства к интегралу для вакуума; это специфика эпохи
наблюдения. То же относится и к приближенному равенству интегралов для излучения
и вакуума.
Численное равенство четырех величин является в (22), конечно,
приближенным; но точность совпадения довольно высока: разброс значений
интегралов не превышает нескольких процентов в относительной логарифмической
шкале: ![]() .
.
Соотношения (22) расширяют
первоначально найденный вариант совпадения фридмановсих интегралов в открытом
мире [50],
добавляя к равенству ![]() и
и ![]() еще и связь этих интегралов с интегралами для двух других форм
космической энергии, т.е. вакуума и темной энергии. Если только это не чистая
арифметическая случайность, совпадение четырех фридмановских интегралов
представляет собой одну из существенных и притом неизменных черт
эволюционирующего мира.
еще и связь этих интегралов с интегралами для двух других форм
космической энергии, т.е. вакуума и темной энергии. Если только это не чистая
арифметическая случайность, совпадение четырех фридмановских интегралов
представляет собой одну из существенных и притом неизменных черт
эволюционирующего мира.
Близкое совпадение фридмановских интегралов означает существование некоей симметрии, объединяющей известные формы космической энергии и сопоставляющей их друг другу. Эта симметрия имеет не временный или случайный характер. Она связана с самой физической природой космических энергий, с их происхождением, и существует так долго, как долго сами эти формы энергии присутствуют в мире. Эта симметрия не затрагивает пространственно-временных отношений и потому является не геометрической, а внутренней, - по терминологии, принятой в физике элементарных частиц.
В слующем параграфе мы скажем о примениении соотношений симметрии (22) для объяснения одной из острых проблем космологии, а затем попытаемся ответить на вопрос о физической природе внутренней симметрии в космологии.
Плотность вакуума, как мы видели, превышает плотности трех других форм
космической энергии, вместе взятые. Слегка дополняя Анти-Дюринга (Кто такой? -
спросит читатель счастливого аспирантского возраста), можно сказать, что в мире
нет ничего кроме движущейся материи и неподвижного вакуума; вакуума даже больше.
Но удивительным образом разница в значениях плотностей не очень велика, особенно
между вакуумом и темной материей, - снова см. данные (2-5). Последнее
означает, что вакуум с его постоянной плотностью лишь сравнительно недавно, при
красном смещении ![]() , согласно формуле (15), оказался
выше темной энергии по эффективной гравитирующей плотности, так что современная
эпоха в эволюции Вселеной - это эпоха продолжающегося перехода от преобладания
темного вещества к преобладанию вакуума.
, согласно формуле (15), оказался
выше темной энергии по эффективной гравитирующей плотности, так что современная
эпоха в эволюции Вселеной - это эпоха продолжающегося перехода от преобладания
темного вещества к преобладанию вакуума.
Как видно из (2-5), не только
эти две плотности, но и все четыре плотности близки друг к другу по порядку
величины. Последнее не может быть объяснено просто тем фактом, что мы измеряем
их в данную переходную эпоху. Действительно, почему, например, плотность
барионов близка к плотности ультрарелятивистской энергии? Эти плотности
изменяются со временем по разным законам: ![]() , - см. формулу (10). Вместе с
более общим вопросом о совпадении всех четырех наблюдаемых космических
плотностей, этот вопрос составляет содержание большой проблемы в современной
космологии, которая называется проблемой космических совпадений. Эта проблема
рассматривается в настоящее время как, возможно, самая острая и принципиальная
для всей физики Вселенной [14,15]. И несомненно важнейший и наиболее
фундаментальный аспект этой проблемы связан с конкретным значением плотности
космического вакуума: почему эта плотность имеет именно то значение, которое
найдено в наблюдениях?
, - см. формулу (10). Вместе с
более общим вопросом о совпадении всех четырех наблюдаемых космических
плотностей, этот вопрос составляет содержание большой проблемы в современной
космологии, которая называется проблемой космических совпадений. Эта проблема
рассматривается в настоящее время как, возможно, самая острая и принципиальная
для всей физики Вселенной [14,15]. И несомненно важнейший и наиболее
фундаментальный аспект этой проблемы связан с конкретным значением плотности
космического вакуума: почему эта плотность имеет именно то значение, которое
найдено в наблюдениях?
Космология не впервые сталкивается с проблемой численных совпадений; у этой темы давняя история, восходящая к обнаруженному Дираком совпадения `больших чисел', - см. об этом в учебниках [6-9]. Но совпадение космических плотностей представляет собой совсем новую страницу этой истории, хотя и в этом своем варианте проблема перекликается с тем, что обсуждалось на тему совпадений ранее.
Упомянутая выше гипотеза квинтэссенции возникла как реакция на проблему совпадения космических плотностей [16]. Оказалось, что можно построить такой вариант модели с квинтэссенцией, что плотность этой гипотетической энергии действительно будет близка к плотности темной энергии в современную эпоху или даже всегда. При этом, однако, не обходится без ряда весьма специальных предположений, которые пока не удается надежно обосновать. Кроме того, не ясно как быть при этом с релятивистской энергией, плотность которой падает при расширении быстрее, чем плотность темной энергии. По этой причине воздержимся здесь от дальнейших подробностей такого подхода к проблеме совпадения плотностей, тем более что, как было сказано чуть выше, наблюдаемая кинематика местного объема Вселенной свидетельствует скорее против квинтэссенции и в пользу космологического вакуума.
Из-заь того что одна из плотностей постоянна во времени (плотность вакуума),
а три другие убывают при расширении, совпадение наблюдаемых плотностей - это,
очевидно, временное явление, случайный эпизод, имеющий место только в
современную эпоху. В другие эпохи этого совпадения плотностей нет. Например, в
ранней Вселенной при возрасте мира ![]() сек плотности барионов и релятивистской энергии были,
соответственно, в
сек плотности барионов и релятивистской энергии были,
соответственно, в ![]() и в
и в ![]() раз больше плотности вакуума, различаясь между собой тоже
на десять порядков величины. Но уже тогда имело место приближенное равенство
интегралов (22), и оно
сохранялось во всей дальнейшей истории вселенной. Это равенство будет
сохраняться и в будущем - вплоть до эпохи распада протонов и/или частиц темной
энергии. За время жизни протона,
раз больше плотности вакуума, различаясь между собой тоже
на десять порядков величины. Но уже тогда имело место приближенное равенство
интегралов (22), и оно
сохранялось во всей дальнейшей истории вселенной. Это равенство будет
сохраняться и в будущем - вплоть до эпохи распада протонов и/или частиц темной
энергии. За время жизни протона, ![]() лет, космические плотности и их отношения меняются на
многие порядки порядков (!), тогда как равенство (22) остается в
силе, будучи равенством независящих от временем величин.
лет, космические плотности и их отношения меняются на
многие порядки порядков (!), тогда как равенство (22) остается в
силе, будучи равенством независящих от временем величин.
С точки зрения соотношений (22),
наблюдаемая близость плотностей вакуума и темной энергии связана лишь с тем, что
современная эпоха - это эпоха перехода от пребладания темной энергии к
преобладанию вакуума. Действительно, из формул (10), (12), (22) имеем для
всех четырех плотностей:
| (23) |
Другой вопрос, почему нам довелось жить именно в эту переходную эпоху; здесь
вступают в игру аргументы совсем другого рода, связанные с антропным принципом
[53,54], и мы в
них вдаваться не будем. Но вопрос о том, почему все четыре плотности оказались
совпадающими, становится теперь ясным: это прямое следствие соотношений
симметрии (22), если
применять их как `первичные' соотношения для вычисления плотностей в эпоху,
когда - временно, и потому случайно - радиус кривизны открытого мира совпал с
величиной ![]() .
.
От эмпирического анализа новейших наблюдательных данных на языке фридмановских интегралов перейдем к вопросу о физической природе приближенного равенства этих интегралов, выражающего внутреннюю симметрию в космологии. Вытекает ли эта симметрия из известных фундаментальных физических законов? Отражает ли она некие более глубокие закономерности в природе?
В поисках ответа на эти вопросы, необходимо обратиться к физике ранней Вселенной, к процессам, которые, как полагают [6-10], могли привести к генерации наблюдаемых форм космической энергии, к `происхождению видов' в космологии, как иногда говорят. В дополнение к тому, что уже было сказано об этом в п.2, приведем здесь очень краткую сводку современных сведений о происхождении и физической природе четырех основных компонент космической среды.
Среди всех ингредиентов космической среды только реликтовое излучение можно
считать простым и полностью понятным по своему физическому происхождению. Это
электромагнитные волны, или фотоны, которые находились в термодинамическом
равновесии с горячей космической плазмой, а при температуре ![]() и возрасте мира
и возрасте мира ![]() млн лет, когда плазма охладилась из-за общего расширения и в ней
произошла рекомбинация, излучение перестало взаимодействовать с веществом. С тех
пор этот газ фотонов продолжает участвовать в космологическом расширении,
оставаясь практически идеально однородным, изотропным и термодинамически
равновесным. Его современная температура измерена исключительно точно, по
космологическим меркам:
млн лет, когда плазма охладилась из-за общего расширения и в ней
произошла рекомбинация, излучение перестало взаимодействовать с веществом. С тех
пор этот газ фотонов продолжает участвовать в космологическом расширении,
оставаясь практически идеально однородным, изотропным и термодинамически
равновесным. Его современная температура измерена исключительно точно, по
космологическим меркам: ![]() К. В каждом кубическом сантиметре Вселенной содержится приблизительно
К. В каждом кубическом сантиметре Вселенной содержится приблизительно
![]() реликтовых фотонов.
реликтовых фотонов.
Вместе с реликтовым излучением в состав релятивистской компоненты космической
среды входят безмассовые и/или легкие нейтрино и антинейтрино (в равном числе).
Их почти столько же по полному числу частиц и античастиц, сколько и
релятивистских фотонов - приблизительно 300 в кубическом сантиметре. Полный
вклад нейтрино в плотность релятивистской компоненты немного меньше вклада
реликтового излучания. Нейтрино и антинейтрино тоже вначале находились в
термодинамическом равновесии с космической плазмой, но из-за малого сечения
взаимодействия с электронами, они отделились от плазмы гораздо раньше, чем
фотоны; это произошло при температуре ![]() МэВ и возрасте мира
МэВ и возрасте мира ![]() сек. Нейтрино слабо взаимодействуют друг с другом, и потому нейтрино и
антинейтрино не аннигилировали и смогли сохраниться до сих пор как еще один
реликт горячего начального состояния мира. Их современная температура около 2 К.
сек. Нейтрино слабо взаимодействуют друг с другом, и потому нейтрино и
антинейтрино не аннигилировали и смогли сохраниться до сих пор как еще один
реликт горячего начального состояния мира. Их современная температура около 2 К.
Гораздо меньше известно о других возможных релятивистских частицах и полях
космологической природы. Среди них наверняка должны присутствовать первичные
гравитоны [49]; их
существование предсказывает также инфляционная модель. Не исключено, что
гравитонов и возможных других частиц, о которых сейчас известно мало или ничего,
может оказаться заметно больше, чем реликтовых фотонов; относительный вклад
нейтрино, гравитонов и др. учитывается множителем ![]() (не слишком определенным) в форуле (5).
(не слишком определенным) в форуле (5).
То `обычное' вещество Вселенной, из которого состоят Земля (и все, что на ней), другие планеты и звезды, - это барионы (протоны, нейтроны) и электроны в числе, равном числу протонов. Что же касается соответствуюших античастиц, т.е. антибарионов (антипротонов, антинейтронов), позитронов, то они присутствуют в ничтожных количествах и обязаны вторичным процессам рождения частиц и античастиц при столкновениях частиц высоких энергий, например, в космических лучах или на мощных ускорителях.
Численную меру такого рода зарядовой асимметрии можно определить, зная
современные значения плотности барионов и реликтового излучения. Дело в том, что
в горячей ранней Вселенной, при высоких температурах, превышающих массу покоя
барионов, барионы и антибарионы (а точнее, составляющие их кварки и антикварки)
должны были иметься в почти равных количествах, причем концентрация (число
частиц в единице объема) тех и других должна была почти точно совпадать с
концентрацией реликтовых фотонов. Позднее, после того как произошла аннигиляция
барионов и антибарионов, избыток частиц над античастицами уцелел и дал
современное наблюдаемое значение плотости барионов. Так как с тех пор число
реликтовых фотонов не менялось (практически) в сопутствующем объеме, то
современное отношение концентрации барионов к концентрации реликтовых фотонов
дает отношение исходного избыточного числа барионов к их исходному полному
числу. При современной плотности барионов ![]() г/см
г/см![]() , их концентрация составляет в среднем
, их концентрация составляет в среднем ![]() в кубическом сантметре. Так получается величина
в кубическом сантметре. Так получается величина ![]() , которая называется космическим барионным числом и служит мерой как
современной, так и изначальной зарядовой асимметрии мира по отношению к барионам
и антибарионам. Именно это малое безразмерное космическое число обеспечило
выживание обычного вещества в ранней эволюционирующей Вселенной и его
существование в сегодняшнем мире.
, которая называется космическим барионным числом и служит мерой как
современной, так и изначальной зарядовой асимметрии мира по отношению к барионам
и антибарионам. Именно это малое безразмерное космическое число обеспечило
выживание обычного вещества в ранней эволюционирующей Вселенной и его
существование в сегодняшнем мире.
Принципиально допустимы две возможности истолкования такого подавляющего избытка частиц над античастицами. Можно принять, что этот избыток существовал в природе с самого начала, т.е. что Вселенная родилась уже резко асимметричной по отношению к частицам и античастицам. Эта точка зрения активно обсуждалась в начале 1960-х годов, причем иногда предполагалось, что первичное превышение числа частиц над числом античастиц могло бы быть одной из фундаментальных констант природы, имеющей тот же статус, что и, скажем, постоянная Планка.
Другой подход к проблеме зарядовой асимметрии мира предполагает, что величина
![]() , характеризующая эту асимметрию, не столь
фундаментальна по своей природе и в действительности должна `выводиться' из
более общих законов физики. В этом случае предполагается, что Вселенная с самого
начала могла быть строго симметричной относительно барионов и антибарионов, а
избыток барионов над антибарионами возник в ранней Вселенной эволюционным путем.
Такая точка зрения была впервые высказана более 30 лет назад в работах [55,56].
Возникновение барионного заряда Вселенной, или, как говорят, космический
бариогенез, требует, согласно [55],
выполнения ряда условий, главное из которых - нестабильность протона. Необходимо
также нарушение C- и CP-инвариантности (т.е. симметрии между частицами С и
комбинированной симметрии С вместе с зеркальной симметрией Р). Кроме того,
требуется нестационарность мира, быстрое космологическое расширение, чтобы
процессы взаимодействия первичных частиц космической среды протекали в
термодинамически неравновестных условиях. Если последнее условие казалось
естественным для ранней Вселенной, то первое из них - нестабильность протона -
представляло собой чрезвычайно смелую по тем временам гипотезу. Но именно эта
гипотеза и сделала, как позже выяснилось, эволюционный подход к проблеме
перспективным и плодотворным.
, характеризующая эту асимметрию, не столь
фундаментальна по своей природе и в действительности должна `выводиться' из
более общих законов физики. В этом случае предполагается, что Вселенная с самого
начала могла быть строго симметричной относительно барионов и антибарионов, а
избыток барионов над антибарионами возник в ранней Вселенной эволюционным путем.
Такая точка зрения была впервые высказана более 30 лет назад в работах [55,56].
Возникновение барионного заряда Вселенной, или, как говорят, космический
бариогенез, требует, согласно [55],
выполнения ряда условий, главное из которых - нестабильность протона. Необходимо
также нарушение C- и CP-инвариантности (т.е. симметрии между частицами С и
комбинированной симметрии С вместе с зеркальной симметрией Р). Кроме того,
требуется нестационарность мира, быстрое космологическое расширение, чтобы
процессы взаимодействия первичных частиц космической среды протекали в
термодинамически неравновестных условиях. Если последнее условие казалось
естественным для ранней Вселенной, то первое из них - нестабильность протона -
представляло собой чрезвычайно смелую по тем временам гипотезу. Но именно эта
гипотеза и сделала, как позже выяснилось, эволюционный подход к проблеме
перспективным и плодотворным.
К концу 1970-х годов стало известно, что распад протона представляет собой
одно из следствий идеи Большого Обьединения, предполагающей единую природу
сильного, слабого и электромагнитного взаимодействий (как известно, мечта
Эйнштейна состояла в том, чтобы построить единую теорию всех четырех
фундаментальных взаимодействий, включая гравитацию). В предыдущем параграфе уже
упоминалось характерное время распада протона; оно очень велико, не меньше ![]() лет. Что же касается нарушения С и СР
инвариантности, то это явление непосредственно наблюдается в распадах
лет. Что же касается нарушения С и СР
инвариантности, то это явление непосредственно наблюдается в распадах ![]() и анти-
и анти-![]() мезонов. Так что соединение новейших идей и экспериментальных фактов
физики элементарных частиц с космологией определенно указывает на реальную
возможность выполнения всех трех необходимых условий бариогенеза в ранней
Вселенной.
мезонов. Так что соединение новейших идей и экспериментальных фактов
физики элементарных частиц с космологией определенно указывает на реальную
возможность выполнения всех трех необходимых условий бариогенеза в ранней
Вселенной.
В конкретных вариантах космологического бариогенеза, которые обсуждались в
последние два десятилетия, изучалась возможность протекания этого процесса в
очень раннюю эпоху, когда температура космического вещества была близка к
характерной энергии Большого Объединения ![]() ГэВ
ГэВ ![]() , а возраст мира
, а возраст мира ![]() сек. Другой вариант - бариогенез при гораздо более низких
температурах, соответствующих характерной энергии электрослабых процессов,
сек. Другой вариант - бариогенез при гораздо более низких
температурах, соответствующих характерной энергии электрослабых процессов, ![]() ГэВ
ГэВ ![]() , когда возраст мира составлял
, когда возраст мира составлял ![]() сек (см. недавние обзоры [57-59]).
сек (см. недавние обзоры [57-59]).
Процитируем в этом месте книгу [9]: `Сценарий
бариогенеза представляет собой один из больших успехов (great triumphs)
соединения физики частиц с космологией ...'. К этому остается только добавить,
что `вывод' космического барионного числа ![]() из фундаментальной теории все еще остается нерешенной задачей. Успешно
показано, что это в принципе возможно, что само число лежит в естественных для
теории пределах величин; но получить его удается пока только в рамках
специальных моделей, а не непосредственно из первых принципов физики. Но может
быть, это число и не настолько в действительности принципиально, что оно
обязательно должно иметь это и только это значение в той единственной Вселенной,
которая нам известна?
из фундаментальной теории все еще остается нерешенной задачей. Успешно
показано, что это в принципе возможно, что само число лежит в естественных для
теории пределах величин; но получить его удается пока только в рамках
специальных моделей, а не непосредственно из первых принципов физики. Но может
быть, это число и не настолько в действительности принципиально, что оно
обязательно должно иметь это и только это значение в той единственной Вселенной,
которая нам известна?
Скажем теперь о темном веществе. До сих пор совершенно не известна, как уже
говорилось в п.2, природа его носителей, и спектр обсуждаемых возможностей
простирается от гипотетических элементарных частиц до звезд-карликов или
массивных черных дыр. Это настолько очевидный и вопиющий пробел в фактических
знаниях о Вселенной, что к этому уже, кажется, ничего особенно и не добавишь. Но
скажем все же и нечто позитивное на эту тему. В духе идей, родственных картине
бариогенеза, можно предположить, что природа скрытого вещества связана так или
иначе с неравновесными процессами в космической среде на ранних этапах
расширения Вселенной. В только что процитированной книге [9], а также и в
книгах [6,8], подробно излагается, например, кинетика закалки частиц и
античастиц в космической среде. Пусть сечение аннигиляции есть ![]() , концентрация частиц
, концентрация частиц ![]() и их средняя скорость
и их средняя скорость ![]() . Тогда характерное время аннигиляции есть
. Тогда характерное время аннигиляции есть
| (24) |
Именно это произошло с нейтрино и антинейтрино (см. выше); но на роль темного
вещества нейтрино не годятся из-за их слишкой малой массы. Однако то же самое
могло бы произойти и с достаточно массивными частицами скрытой массы, - если
только предположить, что носителями темного вещества являются именно
элементарные частицы вместе с античастицами. Такие частицы не должны излучать
электромагнитные волны и вообще взаимодействовать с электромагнитным излучением.
Подобно нейтрино, они могли бы участвовать лишь в слабом (и конечно
гравитационном) взаимодействии. При подходящем значении массы этих частиц они
могли бы обеспечить наблюдаемое значение плотности темного вещества. Одна из
такого рода моделей обсуждается в недавней работе [61], где
делается предположение о том, что закалка частиц темного вещества произошла в
эпоху, когда температура была близка к характерной энергии электрослабых
проценссов ![]() ТэВ. В работе [61]
подчеркивается ключевая роль электрослабых процессов как в физике элементарных
частиц, так и в космологии ранней Вселенной (см. об этом также упомянутые выше
обзоры [57,60]).
ТэВ. В работе [61]
подчеркивается ключевая роль электрослабых процессов как в физике элементарных
частиц, так и в космологии ранней Вселенной (см. об этом также упомянутые выше
обзоры [57,60]).
Наконец, скажем (хотя и не так подробно, как эта тема в действительности
заслуживала бы) о том, что известно о природе космического вакуума и, прежде
всего, о происхождении его наблюдаемой плотности. Малое, но ненулевое значение
плотности вакуума всегда рассматривалось как принципиальная трудность
фундаментальной физической теории [3,4, 60]. В
выражении через планковскую массу, обнаруженная в астрономических наблюдениях
плотность вакуума есть
| (25) |
Речь идет не только о вакууме в космологии, но и о вакууме микромира - как уже упоминалось, это один и тот же физический обьект. На заре релятивистской квантовой теории, когда впервые возник вопрос о природе моря Дирака, о бесконечности его энергии, Гамов говорил, что дираковский вакуум должен обнаружить себя через гравитацию [8]. На семинарах и особенно в коридорах теоретического отдела Ленинградского Физико-технического института в 60-70 гг. (прошлого века) это была одна из неизменных тем оживленных обсуждений, часто со ссылками на Гамова, некогда участника семинаров в тех же стенах. Бесконечна ли плотность вакуума? Но тогда должна быть бесконечно большой кривизна пространства. Если радиус кривизны пространства не меньше расстояния до горизонта, то отсюда вытекает верхний предел плотности вакуума. И шутили вслед за Я.И. Померанчуком: вакуум не пуст, он полон глубокого физического содержания...
Тем временем за океаном вопрос о численном значении плотности вакуума получил
название `проблемы естественности в теоретической физике' [4]. Считалось,
что для такой базовой величины как плотность вакуума нужно ожидать какого-то
весьма сильно выделенного значения, и обсуждаемых вариантов было два - либо
нуль, либо планковская плотность ![]() . Но при огромной планковской плотности кривизна пространства была бы
невообразимо большой; это недопустимо. А если плотность вакуума есть нуль, это
никогда не удастся строго доказать экспериментально...
. Но при огромной планковской плотности кривизна пространства была бы
невообразимо большой; это недопустимо. А если плотность вакуума есть нуль, это
никогда не удастся строго доказать экспериментально...
Действительная плотность, измеренная благодаря гравитационому эффекту вакуума (что и имел в виду Гамов, хотя об анти-гравитации и ускоряющемся расширении он, кажется, не говорил), теперь известна. Она вполне согласуется с соображениями о верхнем пределе, который вытекает из ограничения снизу на радиус кривизны пространства. А в духе прежних аргументов естественности она должна представляться неестественно малой по сравнению с планковской плотностью - на сто двадцать три порядка величины меньше. И бесконечно большой по сравнению с нулем.
С какими еще фундаментальными величинами можно было бы сравнивать плотность
вакуума? Если взять не планковскую массу, а массу, соответствующую Большому
Объединению, ![]() , получим плотность
, получим плотность ![]() ; эта величина на сто порядков превышает наблюдаемое значение плотности
вакуума. Если, далее, принять для тех же целей энергетический масштаб
электрослабых взаимодействий,
; эта величина на сто порядков превышает наблюдаемое значение плотности
вакуума. Если, далее, принять для тех же целей энергетический масштаб
электрослабых взаимодействий, ![]() , плотность будет
, плотность будет ![]() ; разрыв попрежнему очень велик. Из фундаментальных энергетических
масштабов остается еще масштаб кварк-адронных процессов
; разрыв попрежнему очень велик. Из фундаментальных энергетических
масштабов остается еще масштаб кварк-адронных процессов ![]() ; но и он дает недопустимо высокую плотность:
; но и он дает недопустимо высокую плотность: ![]() . Подходящего энергетического масштаба в физике микромира, кажется, не
видно.
. Подходящего энергетического масштаба в физике микромира, кажется, не
видно.
Но обратимся к принципиальной стороне вопроса. Откуда вообще берется энергия
вакуума? Согласно одному из базовых результатов квантовой механики, вытекающему
из принципа неопределенности Гайзенберга, наинизшая энергия квантового
осциллятора не равна нулю, она составляет величину ![]() . Из этих `нулевых колебаний', как их называют, и складывется ненулевая
энергия наинизшего энергетического состояния квантовых полей. Таков
принципиальный ответ на вопрос [8]. Но реально
подсчитать соответствующую суммарную плотность энергии, связанную с нулевыми
колебаниями, квантовая теория поля не позволяет. Если рассмотреть ансамбль
квантовых осцилляторов в качестве модели физических полей и суммировать энергию
нулевых колебаний по всем возможным частотам вплоть до бесконечности, то
результатом и будет бесконечная энергия и бесконечная плотность энергии вакуума.
. Из этих `нулевых колебаний', как их называют, и складывется ненулевая
энергия наинизшего энергетического состояния квантовых полей. Таков
принципиальный ответ на вопрос [8]. Но реально
подсчитать соответствующую суммарную плотность энергии, связанную с нулевыми
колебаниями, квантовая теория поля не позволяет. Если рассмотреть ансамбль
квантовых осцилляторов в качестве модели физических полей и суммировать энергию
нулевых колебаний по всем возможным частотам вплоть до бесконечности, то
результатом и будет бесконечная энергия и бесконечная плотность энергии вакуума.
Чтобы избежать таких расходимостей, прибегают к ограничению диапазона частот
сверху на некотором значении частоты, которое принимается за предельное. Можно,
например, считать, что предельной частоте отвечает планковская энергия ![]() , так что
, так что ![]() . Аргументом в пользу подобного выбора предельной частоты служит тот
несомненный факт, что для энергий, превышающих планковскую, стандартные
представления физики, в том числе и само понятие частоты, теряют обычный смысл.
Но получающаяся при таком подходе плотность вакуума, как можно видеть (хотя бы
из соображений размерности), равна по порядку величины четвертой степени
частоты, и следовательно, она будет иметь значение
. Аргументом в пользу подобного выбора предельной частоты служит тот
несомненный факт, что для энергий, превышающих планковскую, стандартные
представления физики, в том числе и само понятие частоты, теряют обычный смысл.
Но получающаяся при таком подходе плотность вакуума, как можно видеть (хотя бы
из соображений размерности), равна по порядку величины четвертой степени
частоты, и следовательно, она будет иметь значение ![]() , которое, как мы видели, на сто с лишним порядков величины отличается
от реального.
, которое, как мы видели, на сто с лишним порядков величины отличается
от реального.
Зная уже из космологии действительное значение плотности вакуума, нужно
выбрать предельную частоту, а с ней и соответствующий энергетический масштаб
![]() , на уровне
, на уровне
| (26) |
Важнее, однако, то обстоятельство, что характерная длина волны лежит в пределах масштабов, для которых экспериментально проверены законы гравитации. В этом смысле теория наблюдаемого космического вакуума не требует экстраполяции известных законов физики в область масштабов, где эти эти законы остаются непроверенными (ср. с тем, что сказано выше о модели инфляции).
Чтобы найти какой-то сопоставимый масштаб для частоты (26) (а с ней и
для характерной длины ![]() ), обратимся к физике ранней Вселенной. Темп космологического
расширения
), обратимся к физике ранней Вселенной. Темп космологического
расширения ![]() (имеющий ту же размерность, что и частота) дается стандартой формулой
(имеющий ту же размерность, что и частота) дается стандартой формулой
![]() , где под плотностью надо понимать плотность
релятивистской энергии, которая доминирует во Вселенной в первый миллион лет ее
расширения:
, где под плотностью надо понимать плотность
релятивистской энергии, которая доминирует во Вселенной в первый миллион лет ее
расширения: ![]() . Тогда
. Тогда ![]() ГэВ (здесь учтено уже не раз использованное соотношение между
гравитационной постоянной и планковской массой в `микрофизической' системе
единиц;
ГэВ (здесь учтено уже не раз использованное соотношение между
гравитационной постоянной и планковской массой в `микрофизической' системе
единиц; ![]() - температура среды). Темп расширения сравнивается с характерной
предельной частотой при возрасте мира
- температура среды). Темп расширения сравнивается с характерной
предельной частотой при возрасте мира ![]() секунд (пикосекунды) и температуре
секунд (пикосекунды) и температуре ![]() ГэВ. Но последняя величина близка к энергетической шкале слабого
взаимодействия
ГэВ. Но последняя величина близка к энергетической шкале слабого
взаимодействия ![]() . А отсюда вытекает, что предельная частота
. А отсюда вытекает, что предельная частота ![]() численно близка к значению комбинации
численно близка к значению комбинации ![]() . (Если бы мы захотели прибегнуть к экстраполяции законов тяготения до
планковских массштабов, то могли бы сказать, что вакуумный энергетический
масштаб
. (Если бы мы захотели прибегнуть к экстраполяции законов тяготения до
планковских массштабов, то могли бы сказать, что вакуумный энергетический
масштаб ![]() представляет собой гравитационную потенциальную энергию двух масс
величины
представляет собой гравитационную потенциальную энергию двух масс
величины ![]() , разделенных расстоянием, равным планковской длине. Вряд ли, однако,
такое сравнение может быть реально полезным.)
, разделенных расстоянием, равным планковской длине. Вряд ли, однако,
такое сравнение может быть реально полезным.)
При указанной величине ![]() плотность энергии вакуума
плотность энергии вакуума
| (27) |
Интересно, что в уже упомянутой работе [61] выражение
(27) было
получено из сложной теоретико-полевой модели (правда, не без довольно
произвольных и весьма сильных дополнительных предположений). Но если в
соотношении (27) и вправду
есть что-то от сути дела, то природа вакуума должна быть как-то связана с
физикой электрослабых процессов в ранней Вселенной при возрасте мира ![]() сек. В эту эпоху текущий горизонт событий
близок к характерной длине волны
сек. В эту эпоху текущий горизонт событий
близок к характерной длине волны ![]() мм. Возможно, именно в эпоху, когда космическая температура упала до
энергии электрослабых процессов, и произошел последний по времени скачек в
состоянии исходного вакуума (фазовый переход), определивший современное значение
плотности вакуума. Но и независимо от конкретных соображений такого рода можно
полагать, что в первые пикосекунды космологического расширения сложилась вся
дальнейшая судьба Вселенной [3].
мм. Возможно, именно в эпоху, когда космическая температура упала до
энергии электрослабых процессов, и произошел последний по времени скачек в
состоянии исходного вакуума (фазовый переход), определивший современное значение
плотности вакуума. Но и независимо от конкретных соображений такого рода можно
полагать, что в первые пикосекунды космологического расширения сложилась вся
дальнейшая судьба Вселенной [3].
Подчеркнем еще раз, что соотношение (27), хотя оно и выглядит как будто привлекательно, не может, конечно, считаться ни строго доказанным, ни тем более окончательным. Несомненно, что далеко не исчерпаны еще и возможности других известных подходов к проблеме. Существует, например, точка зрения, согласно которой вакуум фермионов и вакуум бозонов имеют разные знаки энергии, так что суммарное значение плотности вакуума могло бы быть нулевым, если имеется строгая симметрия между фермионными и бозонными состояниями (называемая суперсимметрией). А если эта симметрия не точна, то результатом должно быть малое, но конечное значение плотности вакуума (см.[8]). К сокращению плотности вакуума с планковского значения до реального могло бы привести существование скалярного поля, имитирующего вакуумное уравнение состояния с отрицательной энергией [62]. Правда, и эта идея не приводит, как полагают, к последовательному и прямому решению проблемы. Причины трудностей и неудач на этом пути обсуждаются в [4,60]. Поиски новых подходов продолжаются, и из совсем свежих работ отметим модель [63] с тремя вкладами в плотность вакуума: от нулевых колебаний, от пространственной кривизны (низкие энергии) и от конденсата нейтральных бозонов (высокие энергии). Усилия получить разумную плотность вакуума активно развиваются в новейшей теории мембран (см. [64] и имеющиеся там ссылки).
Как видно из сказанного выше, происхождение и вакуума, и не-вакуумных форм космической энергии остается фактически неизвестным. При таких обстоятельствах выяснение физической природы фридмановских интегралов и соотношения симметрии (22) должно казаться делом безнадежным. Так оно в действительности, конечно, и есть. И тем не менее нечто позитивное можно попытаться сказать, не претендуя на многое, и по этому поводу. Разумеется, и тут не избежать тех или иных дополнительных предположений, более или менее правдоподобных или по крайней мере не противоречащих друг другу и надежно установленным фактам; вывод же совпадающих интегралов непосредственно из первых принципов остается нелегкой задачей на будущее, скорее всего, весьма отдаленное.
Расскажем кратко об одной модели [52], которая
способна показать, как - по крайней мере, в принципе - могло бы возникнуть
совпадение фридмановских интегралов в физике ранней Вселенной. Заметим сразу,
что эта модель существенно неполна; она никак не касается трудного вопроса о
природе барионного заряда, и потому фридмановский интеграл для барионов в этой
конкретной модели совсем не фигурирует. Что касается темной материи, но на этот
счет принимается следующее предположение: считается, что ее носителями служат
элементарные частицы с ненулевой массой покоя ![]() , которые подчиняются только слабому взаимодействию и,
конечно, гравитации. Допуская возможность, упомянутую в предыдущем параграфе,
примем, что эти частицы существуют сейчас вместе с соответствующими
античастицами, а аннигиляция не происходит из-за слабости взаимодействия между
частицами и античастицами и из-за их низкой плотности в современную эпоху.
, которые подчиняются только слабому взаимодействию и,
конечно, гравитации. Допуская возможность, упомянутую в предыдущем параграфе,
примем, что эти частицы существуют сейчас вместе с соответствующими
античастицами, а аннигиляция не происходит из-за слабости взаимодействия между
частицами и античастицами и из-за их низкой плотности в современную эпоху.
Реально аннигиляция могла прекратиться уже в весьма раннюю эпоху, когда
температура космической среды упала до значения ![]() (пользуемся, как и выше, системой единиц, в которой
(пользуемся, как и выше, системой единиц, в которой ![]() ), а характерное время аннигиляции (уравнение
(24) при
), а характерное время аннигиляции (уравнение
(24) при
![]() ) оказалось больше возраста мира, т.е. темп аннигиляции
стал ниже темпа космологического расширения или по крайней мере сравнялся с ним:
) оказалось больше возраста мира, т.е. темп аннигиляции
стал ниже темпа космологического расширения или по крайней мере сравнялся с ним:
| (28) |
| (29) |
| (30) |
Кинетика, описываемая этими феноменологическим уравнениями, должна быть
дополнена физикой, ответственной за взаимодействие частиц космической среды в
данную эпоху. В духе сказанного в предыдущем параграфе, будем считать, что
центральную роль в процессе закалки должна играть физика электрослабого
взаимодействия с фундаментальной энергетической шкалой ![]() ТэВ. Более того, примем в соответствии с этим, что
плотность энергии вакуума выражается соотношением (27),
содержащим две фундаментальные энергетические шкалы,
ТэВ. Более того, примем в соответствии с этим, что
плотность энергии вакуума выражается соотношением (27),
содержащим две фундаментальные энергетические шкалы, ![]() и
и ![]() .
.
Согласно общей формуле (12), интеграл
для вакуума с плотностью (27) есть
| (31) |
Рассуждая в том же направлении, нужно предположить, что красное смещение в
данную эпоху должно выражаться в таком случае простой комбинацией тех же двух
фундаментальных констант:
| (32) |
Кроме того, действуя последовательно, нужно считать, что в задаче вообще
должны иметься всего только две фундаментальные константы ![]() и
и ![]() , так что в уравнениях кинетической модели нужно
отождествить массу частицы
, так что в уравнениях кинетической модели нужно
отождествить массу частицы ![]() с
с ![]() . Тогда будем иметь:
. Тогда будем иметь:
| (33) |
| (34) |
По существу, это уже и есть решение задачи, так как ![]() известно, и остается только записать ответ в явном виде:
известно, и остается только записать ответ в явном виде:
| (35) |
Таким образом, приближенное равенство интегралов, а с ним и сама внутренняя симметрия оказываются следствием физических процессов, которые разыгрывались в ранней Вселенной при энергиях, характерных для электрослабого взаимодействия.
При нахождении численного значения интегралов в (35) стоит
принять во внимание одну деталь. Именно, в работе [61] и другой
недавней работе [65], а также и
в ряде более ранних работ, введены в расчеты вместо планковской шкалы
`гравитационная' шкала, или `сниженная' планковская шкала, ![]() , такая что
, такая что ![]() , где
, где ![]() . Множитель
. Множитель ![]() учитывает тот факт, что гравитационная константа
учитывает тот факт, что гравитационная константа ![]() входит в большинство точных космологических
формул в комбинациях вида
входит в большинство точных космологических
формул в комбинациях вида ![]() , или
, или ![]() . (Тем же путем можно учесть и то обстоятельство, что в
формулах кинетической модели должны в действительности стоять такие безразмерные
множители как число степеней свободы и пр. - см. снова учебники [6-9]). Если
последовать этому примеру, то результат (35) можно
представить так:
. (Тем же путем можно учесть и то обстоятельство, что в
формулах кинетической модели должны в действительности стоять такие безразмерные
множители как число степеней свободы и пр. - см. снова учебники [6-9]). Если
последовать этому примеру, то результат (35) можно
представить так:
| (36) |
| (37) |
Остается отметить, что соответствущая формула для красного смещения принимает
вид ![]() . При таком
. При таком ![]() температура в рассматриваемую эпоху
температура в рассматриваемую эпоху ![]() TeV
TeV ![]() , что еще раз непосредственно указывает на центральную
роль электрослабого взаимодействия в данном процессе.
, что еще раз непосредственно указывает на центральную
роль электрослабого взаимодействия в данном процессе.
Напомним, что фридмановский интеграл для барионов остался за рамками данной модели. Между тем его природа тоже, по-видимому, могла бы быть связана с физикой электрослабого взаимодействия в ранней Вселенной. Как упоминалось в предыдущем параграфе, необходимые условия бариогенеза могут быть обеспечны физикой электрослабых процессов. Эти условия способны выполняться в распадах исходных массивных бозонов, если эти распады сопровождаются несохранением барионного заряда.
Сказанное выше, - но прежде и важнее всего, исходные эмпирические данные и соотношения симметрии (22), - позволяют по-новому увидеть место вакуума в общем ряду форм космической энергии. Когда прежде говорилось о близости плотности вакуума к плотностям других форм энергии, приходилось сравнивать константу (плотность вакуума) с переменными величинами, которыми являются плотности не-вакуумных форм энергии. Ясно, что совпадения величин, которые по-разному зависят от времени или не зависят от него вообще, могут быть лишь временными и в этом смысле случайными. Но если смотреть не на плотности, а на соответствующие фридмановские интегралы, то окажется, что рядом с константой для вакуума появляются еще три константы, которые имеют то же космологическое происхождение, и притом все четыре величины даются одной общей формулой (12). Так возникает возможность сопоставления вакуума с другими формами космической энергии на языке постоянных величин той же математической и физической природы. И тогда обнаруживается, что все четыре константы численно близки друг другу.
В контексте фридмановских интегралов наблюдаемое значение плотности вакуума оказывается как раз естественным (вспомним о проблеме естественности в теоретической физике [4]), поскольку именно оно и обеспечивает приближенное равенство вакуумного интеграла интегралам для других форм энергии. Будь эта плотность равна нулю, вакуумный интеграл оказался бы бесконечным; если плотность имела бы планковское значение, интеграл был чрезмерно мал. И это действительно выглядело бы неестественно.
Две острые проблемы космологии и фундаментальной физики - проблема
космических совпадений и проблема естественности - оказываются тесно связанными
друг с другом и сводятся вместе к более общей проблеме внутренней симметрии
космических энергий: Почему ![]() ? Модель закалки, рассмотренная в предыдущем разделе, намечает - в
самом предварительном и предположительном порядке - возможный подход к поискам
ответа на этот вопрос. Выявление нового типа симметрии в космологии, внутренней
симметрии между вакуумом и не-вакуумными формами космической энергии в
пространстве фридмановских интегралов, - одно из прямых и непосредственных
следствий последних наблюдательных открытий в науке о Вселенной.
? Модель закалки, рассмотренная в предыдущем разделе, намечает - в
самом предварительном и предположительном порядке - возможный подход к поискам
ответа на этот вопрос. Выявление нового типа симметрии в космологии, внутренней
симметрии между вакуумом и не-вакуумными формами космической энергии в
пространстве фридмановских интегралов, - одно из прямых и непосредственных
следствий последних наблюдательных открытий в науке о Вселенной.
Эти открытия привели к решительной смене физической картины мира, к совершенно новому пониманию того, что представляет собой современная нам Вселенная. Как оказалось, в ней господствует космический вакуум с его анти-гравитацией, которая заставляет галактики с ускорением разбегаться друг от друга. Но ни галактики, ни его собственная анти-гравитация, ни даже само время не способны воздействовать на нынешний космический вакуум, - он абсолютно неподвижен, неизменен и вечен. Мы неожиданно осознали, что живем в четырехмерном пространстве-времени, которое недавно завершило свою космическую эволюцию и к нынешней эпохе практически достигло идеально регулярного, геометрически симметричного состояния, которое будет затем длиться неограниченно долго.
Мир космического вакуума вплотную подступает к нашей непосредственной области обитания во Вселенной, к Местной группе галактик, где наша Галактика Млечный Путь соседствует с Туманностью Андромеды. Управляемый анти-гравитацией космического вакуума, хаббловский поток разбегания галактик начинается с расстояний всего в несколько мегапарсек от нас и продолжается к горизонту наблюдений, к расстояниям в тысячи мегапарсек, всюду сохраняя свою кинематическую идентичность, единый темп движения, который и задается вакуумом с его одинаковой в пространстве и времени плотностью.
Если поток расширения обязан своим происхождением, как полагают вслед за Глинером, первичному вакууму Вселенной, то его плотность была изначально исключительно высока, превышая его измеренную сейчас плотность на множество порядков величин. Из-за этого вакуум и сам был способен изменяться, эволюционировать, порождая при этом `обычное' вещество, не-вакумные формы космической энергии. Эта эволюция первичного вакуума завершилась в первые пикосекунды существования мира, оставив после себя многокомпонентную космическую среду, в которой вакуум и не-вакуумные энергии оказались в итоге согласованными друг с другом, симметричными по отношению друг к другу: их неизменные во времени природные физические характеристики, фридмановские интегралы, с тех пор численно близки и будут оставаться близкими до тех пор, пока сами эти формы энергии сохраняются в природе.
Гипотеза о физическом вакууме и космической анти-гравитаци, выдвинутая Эйнштейном на заре современной космологии, вновь оказывается в центре внимания этой науки. Выясняется, что она исключительно богата реальным физическим и астрономическим содержанием, о чем ее автор мог, вероятно, только смутно догадываться. Но главное состоит в том, что гипотеза Эйнштейна верна.
[1] Riess A G et al. Astron. J 116 1009 (1998); Perlmutter S et al. Astrophys. J 517 565 (1999)
[2] Ландау Л Д, Лифшиц Е М Теория поля, Москва, Наука (1967)
[3] Окунь Л Б Лептоны и кварки, Москва, Наука (1982); Окунь Л Б Физика элементарных частиц, Москва, Наука (1988)
[4] Weinberg S Rev. Mod. Phys. 61 1 (1989)
[5] Фридман А А УФН 80 439, 447 (1963)
[6] Зельдович Я Б, Новиков И Д Строение и эволюция Вселенной, Москва, Наука (1975)
[7] Peebles P J E Principles of Physical Cosmology, Princeton Univ. Press, Princeton (1993)
[8] Долгов А Д, Зельдович Я Б, Сажин М В Космология ранней Вселенной, Москва, МГУ (1988)
[9] Kolb E W, Turner M S The Early Universe, NY, Addison-Wesley (1990)
[10] Линде А Д Физика элементарных частиц и инфляционная космология, Москва, Наука (1990)
[11] Глинер Э Б ЖЭТФ 49 542 (1965), ДАН СССР 192 771 (1970)
[12] Старобинский А А Письма ЖЭТФ 30 719 (1979)
[13] Carol S astro-ph/0004075 (2000)
[14] Парийский Ю Н Current Topics in Astrofundamental Physics (eds. N Sanches & A Zichichi) NATO ASI Series, Vol.511, p.443 (2000)
[15] Wang L, Caldwell R R, Ostriker J P, Steinhardt P J Astrophis. J 530 17 (2000)
[16] Caldwell R R, Steinhardt P J Phys.Rev. D 57 6057 (1998)
[17] Зельдович Я B УФН 80 537 (1963)
[18] Чернин А Д Астрон. ж. 42 1124 (1965)
[19] Тропп Э А, Френкель В Я, Чернин А Д Александр Александрович Фридман, Москва, Наука (1988)
[20] Grib A A Early Expanding Universe, S-Petersburg, Friedmann Lab. (1995)
[21] Baryshev Yu V et al. Vistas Astron. 38 419 (1994)
[22] Baryshev Yu V et al. Fractals 6 231 (1998)
[23] Wu K K S, Lahav O, Rees M J Nature (London) 397 225 (1999)
[24] Teerikorpi P Ann. Rev. Astron. Astrophys. 35 101 (1997)
[25] Gromov A et al. Grav. Cosm. 7 (2001)
[26] Kogut A et al. Astrophys. J. 419 1 (1993)
[27] Караченцев И Д и др. Астрон. ж. 44 150 (1998)
[28] Joyce M. et al. Europhys. Lett. 49 416 (2000)
[29] Sylos Labini S, Montuori M, Pietronero L Phys. Rep. 293 61 (1998)
[30] Караченцев И Д УФН (2001)
[31] Sandage Astrophys. J 527 479 (1999)
[32] Sandage A, Tammann G, Hardy E Astrophys.J 172 253 (1972)
[33] Sandage A Astrophys. J 307 1 (1986)
[34] Караченцев И Д, Макаров Д И Астрофизика 44 5 (2001)
[35] Teerikorpi et al. Astron. Astrophys. 334 395 (1998)
[36] Chernin A D, Teerikorpi P, Baryshev Yu V Adv. Space Res. (2001)
[37] Baryshev Yu V, Chernin A D, Teerikorpi P Astron. Astrophys. (in press)
[38] Karachentsev I, Makarov D. Astron.J 111 794 (1996)
[39] Караченцев И Д, Теерикорпи П, Чернин А Д (готовится к печати)
[40] Chernin A D, Nagirner D I, Starikova S V (in press)
[41] Зельдович Я Б Astron. Astrophys. 5 84 (1970)
[42] Ekholm T et al. Astron. Astrophys. 368 L17 (2001)
[43] Einasto J New Astron. Rev. 45 355 (2001)
[44] Einasto J et al. Astrophys. J. 519 441 (1999)
[45] Governato F et al. New Astron. 2 91 (1997)
[46] Zaslavsky G M, Sagdeev R Z, Cherninkov A A, Usikov D A Weak Chaos and Quasiregular Patterns, Cambridge, Cambridge Univ. Press (1999)
[47] Chernin A D, Valtonen M J New Astron. Rev. 42 41 (1998)
[48] Einasto J et al. Nature (London) 385 139 (1997)
[49] Грищук Л П и др. УФН 171 3 (2001)
[50] Чернин А Д Письма ЖЭТФ 8 633 (1968), Nature (London) 220 250 (1968)
[51] Gamow G Phys. Rev. 74 505 (1948)
[52] Чернин A Д astro-ph/0101532
[53] Розенталь И Л Элементарные частицы и структура Вселенной. Москва, Наука (1984), УФН 167 801 (1997)
[54] Weinberg S Phys. Rev. Lett. 59 2607 (1987)
[55] Сахаров А Д Письма ЖЭТФ 5 32 (1967)
[56] Кузьмин В А Письма ЖЭТФ 13 335 (1970)
[57] Долгов А Д Phys. Rep. 222 309 (1992)
[58] Рубаков В А, Шапошников М E УФН 166 493 (1996)
[59] Cohen A G et al. Ann. Rev. Nuc. Part. Phys. 43 27 (1993)
[60] Рубаков В А УФН 169 1299 (1999)
[61] Arkani-Hamed N, Hall L J, Kolda C, Murayama H Phys. Rev. Lett. 85 4434 (2000)
[62] Долгов А Д The Very Early Universe, eds. G W Gibbons et al., Cambridge Univ. Press (1982) p.82
[63] Розенталь И Л, Архангельская И В Астрон. ж. (в печати)
[64] Tye S-H H, Wasserman I Phys. Rev. Lett. 86 1682 (2001)
[65] Kawasaki M, Yamaguchi M, Yanagida T Phys. Rev. Lett. 85 3572 (2000)