
 |
© 2003 Optical Society of America OCK codes:
270.0270,260.0260.
РЕВИЗИЯ КОНЦЕПЦИИ ФОТОНА
Ашок Матукришнан, Марлен Скалли и Сухайл
Зубайры
Понятие фотона - один из наиболее обсуждаемых вопросов в истории физической науки. Около тридцати лет тому назад, мы опубликовали статью в “Физике сегодня” под названием "Понятие Фотона" [1], в которой мы описали "фотон" как классическое электромагнитное поле плюс колебания, связанные с вакуумом. Тем не менее, в последующем, потребовалось предусмотреть, что фотон как собственно кванто-механическая сущность, чья основная физика значительно более глубокая, нежели может быть объяснено простой формулой – “классическая волна плюс вакуумные колебания”. Эти идеи и расширения нашего концептуального понимания обсуждены подробно в нашей последней книге по квантовой оптике [2]
. В этой статье мы вновь рассматриваем понятие фотона, основанное на примерах из этого и других источников.
Ф
отон является концептуальной квинтэссенцией двадцатого столетия, непосредственно связанной с рождением квантовой механики и квантовой электродинамики. Тем не менее, корни идеи, можно сказать, значительно более древние, на столько же, как историческая дискуссия о природе света сама - независимо это волна или частица - которая свидетельствует о раскачивании маятника идеологии о его представлении еще из древности. Переход от классического представления света к квантовому является пока некоей дихотомией, где необходимо квантовать электромагнитное поле (к тому же квантовать материю). Решение лежит в нахождении ключа в поведении квантовых полей света, которые не входят в классическое поле, как например, вакуумные колебания и квантовое переплетение, которые необходимы для квантовой теория излучения. [2, 5]. Тем не менее, точное понимание понятия "фотона" не является легкой задачей, недаром Альберт Эйнштейн говорил:"Сейчас каждый подлец думает, что он знает, что такое фотон, но он заблуждается."
Поэтому, мы должны приступить к обсуждению с осторожностью и некатегоричностью. Как говаривал Виллис Лэмб
: [6]" Что мы будем делать теперь? Мы можем и должны использовать квантовую теорию излучения. Ферми показал, как это делать в случае с линиями Липпмана. Идея - проста, но при детальном рассмотрении - ошибочна. Хорошее понятие и масса практики делают наше положение легче. Начните с того, что решите общие вопросы этой дискуссии. Решите, какте нормальные способы необходимы для требуемого решения. Решите как моделировать источники света и как они управляют системой.
"Мы приступаем к тому, чтобы объяснить понятие фотона специфическими экспериментами (реальными и воображаемыми), которые демонстрируют его свойства и проливают свет на значение "фотона." В особенности, мы собираемся кратко просмотреть историю дискуссии о волне - частице и затем дать семь наших любимых примеров, каждый из которых разъясняет некоторый ключевой аспект квантовой природы света. Два лица фотона, на которых мы фокусируем внимание - вакуумные колебания (как в нашей более ранней работе [1]), и аспекты многочастичных корреляций (как в нашей последней книге [2] ). Примеры первого - спонтанная эмиссия, Лэмбовский сдвиг, рассеяние атомов вакуумным полем на входе в микромазер. Примеры второй природы включают
квантовые удары, квантовый стиратель и корреляцию фотона в микроскопии. Наконец, на примере двухбазовой понижающей интерферометрии мы покажем, что сущность обоих лиц фотона объединена и объяснена.В конце статьи, мы вернемся к основным вопросам относительно природы света как волновой частицы в контексте дискуссии: Что такое фотон и где он? На первый вопрос, мы отвечаем в словами Роя Глобера
:"Фотон – это то, что детектирует фотодетектор."
На второй вопрос (о локальности фотона), ответ будет таков: "фотон там, где фотодетектор его обнаруживает." В принципе, детектор мог быть микроскопическим объектом как например, атом. Руководствуясь этой точкой зрения, мы адресуем вас к многочисленным обсуждениям прооблемы существования фотона как функции ψ(r, t) [2, 7, 8]. Аргументируя противоположный взгляд, мы покажем, что понятие волновой функции фотона возникает естественным образом из квантовой теории фотодетектирования (смотри [2], гл.1). Очень много дается взглядом на проблему через интерференцию, изучение свойств переплетения света как однофотоной , так и связанной двухфотоной “волновой функцией” [2].
Свет – волна или частица?
Проблема природы света является такой же старой, как сама истории науки. Для древних греков и арабов дискуссия концентрировалась на связи между светом и зрением. Тактильная теория, которая сводилась к тому, что наше зрение осуществляется нашими глазами, имеющими способность "касаться" чего-то или чувствовать что-то на расстоянии, постепенно преобразовывалась в теорию эмиссии, которая постулировала, что зрение происходит от освещения объектов, испускающих энергию, которая чувствуется нашими глазами. Это смещение парадигмы произошло главным образом благодаря арабскому ученому XI столетия Абу Али ибн аль-Хайфаму (или “Альхазену”), который заложил фундамент классической оптики исследованиями по преломлению и дисперсионным свойствам света.
Затем мыслители Ренессанса в Европе видели свет как поток частиц, возможно поддерживаемый
эфиром, невидимой средой, заполняющей все пустое пространство и все прозрачные вещества.В семнадцатом столетии, Пьер Ферма ввел принцип наименьшего времени, чтобы учесть явление рефракции. Эквивалентно, его принцип утверждает, что луч света выбирает путь, который минимизирует оптическую длину пути между двумя точками в пространстве
:|
|
(1) |
где n = c/v (пространственно измененяющийся) коэффициент преломления, который определяет скорость частицы света, и
Христиан Гюйгенс, с другой стороны, современник Ньютона, был прочным защитником волновой теории света. Он сформулировал принцип (что теперь носит его имя), который описывает распространение волн как интерференцию второстепенных элементарных волн, возникающих из точечных источников в волновом фронте.
Это завладело математическим гением Августина Френеля, который 150 лет позже, реализовал это открытие, включив строгую разработку в теорию волновой дифракции. Свет не формирует точные, геометрические тени, которые были бы характерными для частицы, но изгибается вокруг препятствий и углов.
Оживление волновой теории в начале девятнадцатого века [1] было осуществлено Томасом Юнгом. В 1800, выступая перед Королевским Обществом Лондона, Юнг говорил об аналогии света и звука, и объявил позже, что двухщелевой эксперимент интерференции должен окончательно продемонстрировать волновую природу света (см. рис. 1). Трудно для современного читателя представить себе как это предложение было противно интуитиции в то время.
Идея того, что экран единообразно освещенный под единственной апертурой мог бы показать темные дополнительные полосы при введении второй апертуры, что дополнение больших источников света могло бы закончиться меньшим освещением - было слишком парадоксально для аудитории Юнга, чтобы быть усвоенным.
Подобно этому, теория дифракции Френеля была принята со скептицизмом жюри призового комитета в Париже, в 1819. В частности, уважаемый Пьер Симон де Лаплас отнесся к волновой теории очень скептически. Его протеже, Симеон-Денис Пуассон, обнаружил, что, по-видимому, абсурдно то, что теория подразумевала яркую точку в центре тени освещенного непрозрачного диска, теперь известной как Пуассоновская точка.
Сопротивление переключения с корпускулярного на волновое описание света этими сверхвыдающимися учеными начала девятнадцатого столетия указывает на большую разницу между этими двумя понятиями. Это было предверием борьбы, которая придет через сотню лет с приходом квантовой механики.
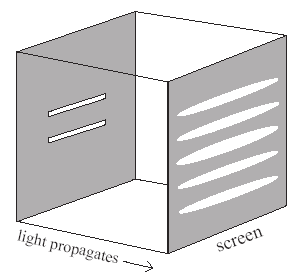
Фиг. 1. Двухщелевой эксперимент Юнга - Свет проходит через две щели в ящик и распространяется вдоль двух путей в данную точку на экране, создающем и разрушающем интерференцию. Когда единственный фотон является источником в щелях, он обнаруживается самой большой вероятностью в пиках интерференции, но никогда в узлах интерференции.
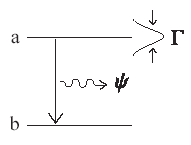
. 2. Спонтанная эмиссия – Двухуровневый атом, с шириной линии верхнего уровня Г спонтанно выдает фотон. Колебания в вакуумном поле вызывают переход возбужденного состояния электрона в основное состояние в течение характеристического времени t [1].Рис
Волновая теория действительно пришла к своему собственному виду в конце 19-го столетия в работах Джеймса Клерка Максвелла. Его четыре уравнения, известных всем студентам-физикам последнего курса обучения, первая завершенная теория излучения. Получившая подтверждение в экспериментах Генриха Герца, теория Максвелла объединила разрозненные явления электричества и магнетизма и придала физический смысл поперечной поляризации волн света. Далеко идущий успех теории объясняет то высокомерие физиков конца девятнадцатого столетия, многие из которых верили, что были действительно только два "облачка" на горизонте физики в начале 20-го столетия. Интересно, что они оба относились к свету.
Первое облачко, а именно: нулевой результат эксперимента Майкельсона-Морли, привел к специальной теории относительности, которая покончила с классической механикой и явилась камнем преткновения классической физики.
Вторым облаком была ультрафиолетовая катастрофа Рэлея-Джинса (UV)-катастрова и природа чернотельной радиации, проведшие к приходу квантовой механики, которая была радикальным изменением в физическом мышлении. Так как обе этих проблемы включали ЭМ-поле, то это не могло (вначале) привести к понятию фотона.
То есть […] до Макса Планка не могло быть обращения к природе света, состоящего из частиц к объяснению наблюдаемых явлений. Относительность была строго классической, и Планк, квантовавший энергии осцилляторов на стенках полости, не имел ввиду поля [9].
Рождение теории света как частиц и начало современного понятия фотона, является заслугой Эйнштейна. В его статье 1905 на о фотоэлектрическом эффекте [10], где рассматривалась эмиссия электронов с металлической поверхности, освещенной УФ-лучами, Эйнштейн постулировал, что свет испускается дискретными порциями, или долями энергии,
заимствуя гипотезу Планка пятилетней давностиE =![]()
где ![]() была циклическая частота и
была циклическая частота и
![]() константа Планка разделенная
на 2
константа Планка разделенная
на 2![]() .
.
Это введение в природу света из частиц в физическое рассуждение, не как локализация в пространстве в виде частиц Ньютона, но как дискретность в энергиях. Но ирония судьбы заключается в том, что Эйнштейн получил идею фотона из физики фотоэлектрического эффекта. Фактически, это можно показать, что сущность фотоэлектрического эффекта не требует квантования излучения поля
, [11], но это заблуждение повторяемое из учебника в учебник, въелось в ум целого столетия [12]."Фотоэлектрическое уравнение Эйнштейна сыграло ненормально большую роль в разработке современной квантовой теории. Но несмотря на общность и многие успешные приложения, которые были сделаны в физических теориях на основе уравнения
:|
|
(2) |
как мы должны увидеть вскоре, основанное на понятии излучения, понятие
“долей света” - полностью совместимо с наиболее фундаментальными концепциями классической электромагнитной теорией излучения.Далее мы вновь коснемся фотоэлектрического эффекта и установим его правильное положение в контексте теории излучения. Как гипотеза Планка, так и Эйнштейновская интерпретация следуют из соображений того, как обмениваются энергией излучение и вещество. Вместо электромагнитной волны с непрерывно меняющейся амплитудой классического осциллятора, мы имеем дискретную картину света соответствующей частоты или поглощение и излучение квантовым осциллятором, как например, атомом на стенках полости, или на металлической поверхности. Эта, по-видимому, близкая связь между энергетическим квантованием и взаимодействием излучения с веществом мотивировала оригинальное слово "фотон" Гильберта Льюиса в 1926 [13]:
"Должно казаться неподходящим, говорить об одной из таких гипотетических сущностей, как частица света, квант света, или корпускула света, если мы должны допустить то, что он тратит только малую долю своего существования как носитель лучистой энергии, тогда как остальная часть времени та, в которой он остается важным структурным элементом в пределах атома... Cледовательно, я позволяю себе предложение для гипотетического нового атома
Энергетическое квантование является сущностью старого кванта, старой квантовой теории, атома, предложенного Нильсом Бором. Говорят, что электрон занимает дискретные орбиты с энергиями
Ei и Ej с переходами между ними, вызванными фотоном соответствующей частотыv
= (Ei —Ej) /Удачная интерпретация этого квантования с точки зрения волн материи была дана Луисом де Бройлем, который аналогией со стоячими волнами в полости доказал, что длины волн электронов на каждой Боровской орбите, квантованных количеством целых длин волн, должны иметь циклические орбиты соответствующего радиуса. Это стало толчком для Эрвина Шрёдингера, чтобы ввести его знаменитое волновое уравнение для волн материи и оснований для (нерелятивистской) квантовой механики материальных систем.
Квантовая механика дает нам новую перспективу в корпускулярно-волновой дискуссии вокруг двухщелевого эксперимента Юнга (рис.1). В парадигме квантовой интерференции добавились стохастические амплитуды, связанные с альтернативными путями через интерферометр. Свет (или материя) не волна и не частица, но промежуточная сущность, которая подчиняется принципу наложения.
Когда единственный фотон проходит через щели, он регистрируется как событие наподобие точки на экране (измеренное скажем, ПЗС-матрицей). Накопление таких событий, повторяющих испытания строит вероятностный образ щели, который соответствует классической волновой интерференции. Однако, если организовать сбор информации о том, через какую прорезь проходит фотон, интерференционная картина исчезает. Таким образом, с позиции комплементарности, как волны, так и частицы имеют равную законную силу. Мы возвратимся к этой
мысли ниже.Полуклассический взгляд
Взаимодействие излучения и вещества - ключ в понимании природы света и понятии фотона.
С полуклассической точки зрения, понятие света – классическое, и только вещество квантованно. Другими словами, имеется обращение в равной степени к волновой теории света (уравнения Максвелла последовательно объединяются с волновой теорией вещества по уравнениям Шрёдингера). Это дает в высшей степени точное описание большого класса явлений, включая фотоэлектрический эффект, стимулирующий эмиссию и поглощение, эффекты насыщения и нелинейную спектроскопию, явления распространения импульса, "фотонные эхо", и т.п.. Многие свойства лазерного света, такие как например частотная избирательность, фазовая когерентность и направленность, могут быть объяснены в пределах этих рамок [14]. Рабочей лошадкой полуклассической теории является двухуровневый атом, особенно проблема его взаимодействия с синусоидальной световой волной [15]. В дейст-вительности, реальные атомы имеют массу уровней, но двухуровневая аппроксимация склонна к выделению особого преобразования вблизи резонанса с частотой поля
v. Таким образом, энергия разделения уровней может быть принята как Ea — Eb =Давайте приложим полуклассический анализ к фотоэлектрическому эффекту, который придал оригинальный импульс для квантования света. Есть три наблюдаемые характеристики этого эффекта, которые нам надо учесть. Сначала, когда свет освещает поверхность фотоэмиссии, электроны извлекаются с кинетической энергией
E, равнойВсе три наблюдения могут быть номинально объяснены применением полуклассической теории в самом первом приближении как волновое взаимодействие атом - поле
V(t) = -eEor [11]. Это Золотое Правило Ферми для вероятности перехода электрона с основного уровня в атоме в бесконечность:|
|
(3) |
где
erkg - матричный элемент диполя между начальным и конечным состоянием.Теперь, записывая энергию
Ek — Eg как E + Φ, мы видим чтоТам где мы отходим от классической интуиции для света возникает тонкая проблема, связанная с третьим фактом, а именно: имеется незначительная задержка времени между воздействием света и эмиссией фотоэлектрона. Но это вроде бы понятно с атомной точки зрения - электрон имеет конечную вероятность возбуждения даже в течение очень короткого времени - этот аргумент ломается тогда, когда мы рассматриваем вопрос вовлекая поле. То есть, если мы упорствуем в мышлении о поле классически, энергия не сохраняется. За интервал времени
t классическое поле E0 вносит изменение энергииДля этой и других причин (смотри следующий раздел) нам надлежит дополнение эпистемологии теории Максвелла квантованным видом электромагнитного поля, что будет полностью учитывать вероятностную природу света и присущих ему колебаний. Это именно то, что делал в течение года 1927 Поль Дирак
, когда понятие фотона, впервые было установлено в логическом смысле, и родилась квантовая теория излучения [16]. Это последовало в 1940-х замечательно успешной теорией квантовой электродинамики (КЭД) - квантовой теория взаимодействия света и вещества, которая достигла беспрецедентной цифровой точности в предсказании экспериментальных наблюдений. Тем не менее, не позже, чем через двадцать лет мы должны были возвратиться на полный круг саги полуклассической теории, с Эдом Джейнсом, поставившим вопрос о потребности в квантовой теории излучения в 1966 на конференции по когерентности и квантовой оптике в Рочестере, штат Нью-Йорк."
Физика идет вперед на плечах скептиков, а не верующих, и я сомневаюсь в необходимости КЭД,"- объявлял Джэйнс. С его точки зрения, полуклассической теории или неоклассической теории с дополнением поля реакции излучения, действующего на атом было достаточным, чтобы объяснить Лэмбовский сдвиг, который был единственным существенным подтверждением квантования поля Дирака и теории КЭД (смотри ниже). Другим побочным продуктом конференции был Питер Франкен, вызванный Джэйнсом на пари. Один из нас (MOS) вспомнил слова Франкена на конференции: "Вы были черезчур богатым человеком, а теперь - я, и я говорю: выкладывайте свои денежки с вашего лицевого!" Они держали пари на $100 по поводу того, мог или не мог Лэмбовский вычисляться без КЭД. Джэйнс выиглал пари, в котором Уиллис Лэмб согласился быть судьей.
В 1960-е и 70-е Джэйнс и его сотрудники сообщали о частичном успехе с предсказанием Лэмбовского сдвига используя неоклассическую теорию [17]. Они смогли найти качественную связь между сдвигом и физикой реакции излучения при отсутствии квантования поля или вакуумных колебаний, но не смогли произести точный цифровой прогноз, который бы мог сверяться с экспериментом. По этой причине, на конференции 1978 в Рочестере, Лэмб решил поставить в пари на Франкена. Счет в этом пари был подведен Джэйнсом в его докладе на конференции [18]. И наконец, КЭД приняла вызов полуклассической теории, и вакуумные колебания были на самом деле "очень реальными вещами" подсчитанными с помощью КЭД.
Семь примеров
Наши первые три примера ниже - иллюстрация дейст-вительности колебаний вакуума в электромагнитном поле, как это обнаружено в атомной физике. Это означает, что фотон в этом контексте приобретает стохастику. Кое-кто говорит о классическом ЭМ-поле с колебаниями из-за вакуума. Чтобы снять сомнения, связанные с невозможностью наблюдать эти колеба-ния с фотодетектора, скажем, что они делают свое присутствие чувствуемым, например, тем что траектории атомных электронов "шевелятся" этими произвольными вакуумными силами.
1. Спонтанная эмиссия
В явлении спонтанной эмиссии
[19] атом в возбужденном состоянии переходит в основное состояние и спонтанно излучает фотон (смотри Рис.2). Эта "спонтанная" эмиссия в некотором смысле является стимулированной эмиссией, где стимулирующее поле являляется колебаниями вакуума. Если бы атом оставался в возбужденном состоянии и поле было бы классическим, и атом никогда не развивал бы дипольный момент и никогда не излучал бы. В этом смысле, полуклассическая теория не принимает во вниманте спонтанную эмиссию. Тем не менее, когда вакуумные колебания учитываются, концептуально, мы можем думать о том, что атом может стимулироваться, чтобы выдавать излучение колебательного поля, и отдача излученного света будет возвращать атом в основное состояние, вызывая разрушение возбужденного состояния. Таким образом, мы понимаем спонтанную эмиссию как следствие вакуумных колебаний.2. Лэмбовский сдвиг
Возможно величайший триумф квантования поля - это объяснение Лэмбовского сдвига [20] между, например, уровнями 2
s1/2 и 2p1 /2 в атоме водорода. Релятивистская квантовая механика предсказывает, что эти уровни должны вырождаться, в противоречии с экспериментально наблюдаемым частотным разделением около 1GHz. Мы можем понять сдвиг интуитивно [21], представляя что электрон вынуждается колебаться возле своей первоначальной позиции в атоме из-за произвольных ударов окружающего его, колеблющегося вакуумного поля (см. рис.3). Его среднее смещение σ равно нулю, но квадратичное смещение σ2 немного не равно нулю, в результате чего электрон "чувствует" немного другое кулоновское притяжение от положительно заряженного ядра, нежели нормальное. Этот эффект более силен вблизи ядра, где потенциал Кулона ослабевает более круто, но орбитальные воздействия различны. Это обнаруживается как Лэмбовский сдвиг между уровнями.3. Микромазер - рассеяние вакуума
Микромазер состоит из единственного атома, взаимодействующего с одномодовым квантовым полем в высокодобротной полости
[22]. Интересная новая перспектива в вакуумных колебаниях дается недавним примером возбужденного атома, рассеиваемого эффективным потенциальным барьером, созданным вакуумным полем в полости (см. рис. 4) [23].Когда движение атомного центра масс квантуется, и атомы движутся достаточно медленно (их кинетическая энергия меньше энергии взаимодействия атом - поле), показано, что они могут подвергнуться отражению из полости в то время, когда она совершенно пустая, то есть в ней нет фотонов. Отражение атомов происходит из-за дискретного изменения в силе связи с вакуумными колебаниями происходящими в полости. Этот тип отражения - краевая прерывность - общая в волновой механике. Что интересно! Сущность этого примера в том, что отражение является следствием крутого поворота в точке связи вакуума с внутренней поверхностью полости. Теперь честно рассмотрим эту физику, как другое проявление эффекта вакуумных флуктуаций, на этот раз - влияния на динамику центра масс атома.
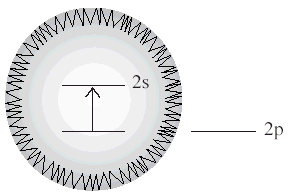
. Лэмбовский сдвиг - схематическая иллюстрация Лэмбом состояния водорода 2s 1/2 относительно состояния 2p1/2.Фиг. 3
Интуитивное понимание сдвига, как произвольного подбрасывания электрона в 2s из орбитально нулевой точки флюктуацией вакуумного поля.
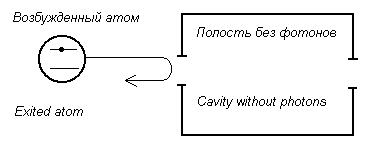
Вакуумное рассеяние - возбужденный атом подходящий к пустой полости может отражаться или достаточно замедлить свою скорость. Вакуумное поле полости служит в качестве эффективного потенциального барьера для центра масс волновой функции атома.Фиг. 4.
Наши следующие три примера включают понятие многочастичного переплетения, которое является отличительной чертой квантового электромагнитного
поля. Исторически, межчастичные корреляции играют ключевую роль в фундаментальных тестах квантовой механики, как например, ЭПР-парадокс, неравенства Белла и квантовый стиратель. Эти примеры иллюстрируют действительность квантовых корреляций в многофотонной физике. В последние годы переплетённые фотоны были ключевым моментом в приложениях квантовой информации и вычислениях, развитии новых технологий как например, корреляционной фотонной микроскопии (смотри ниже).4. Квантовые биения
В общих чертах, биения возникают всякий раз, когда две или
больше частот волны одновременно присутствуют. Когда атом в возбужденном
состоянии подвергается релаксации по двум путям перехода, ожидается, что
излученный свет получаемый в этом процесе, где ожидаются биения, будет иметь
разные частоты ωα - ωβ,
дополнительно к частотам
индивидуального перехода ωα и ωβ
. Тем не менее, когда
единственный атом релаксирует, биения присутствуют только, когда два конечных
состояния атома идентичны (см. Рис. 5). Когда конечные состояния являются
разными, квантовой теорией предсказывается отсутствие биений [24]. Это так,
поскольку два канала релаксации заканчиваются разными атомными состояниями
[![]() or
or ![]() [ или на рисунке 5(b)].
Теперь мы знаем траекторную информацию фотона, и нам нужно только проверить,
какой фотон (α или β) был выдан - то есть
переплетение между атомом и квантованным полем уничтожает интерференцию.
Классическая электродинамика и vis-а-vis полуклассическая теория не могут
объяснить "исчезновение" биений.
[ или на рисунке 5(b)].
Теперь мы знаем траекторную информацию фотона, и нам нужно только проверить,
какой фотон (α или β) был выдан - то есть
переплетение между атомом и квантованным полем уничтожает интерференцию.
Классическая электродинамика и vis-а-vis полуклассическая теория не могут
объяснить "исчезновение" биений.
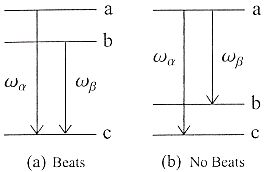
Фиг. 5
. Квантовые биения - a) Когда единственный атом релаксирует с двух верхних уровней на общий более низкий уровень. Две частоты перехода производят биение в излучаемом фотоне, b) Биения отсутствуют когда более низкие уровни различны. Поэтому конечное состояние атома обеспечивает нас точной информацией о маршруте фотона релаксации.
5.
Квантовый стиратель и дополнительностьВ квантовом стирателе [25] информация о пути интерферирующей частицы стирается путем манипуляции второй, спутанной частицей. Дополнительность выполняется не посредством принципа неопределенности (через процесс измерения), но квантовой корреляцией между частицами [26]. Это понятие может реализовываться в контексте двухфотонной интерферометрии [27-29]. Рассмотрим установку, показанную на рисунке 6, где один из двух атомов i = 1, 2 выдает два фотона фi, и γi. Интерференция наблюдается в ф только тогда, когда пространственно источник не может быть различён, то есть, когда срабатывает детектор D1 или D2. Стирание происходит когда фотон отражен (а не пропущен) через лучевые делители BS1 или BS2, что в эксперименте происходит после того, как ф фотон был обнаружен. Таким образом, квантовое переплетение между фотонами допускает реализацию “задержанного выбора” [30], который не может быть смоделирован классической оптикой.
6. Фотонно-корреллированная микроскопия
Новые явления интерференции возникают из coотношений запутанных фотонов второго порядка, как например, возникновение из спонтанного каскадного излучения трехуровневого атома (где выданные фотоны согласовываются по частоте и времени эмиссии). Когда два таких атома пространственно разделены и один из них подвергается разрушению, двухфотонное измерение способно к высокоразрешающей спектральной микроскопии на уровне атомных структур.[31]
Можно показать, что разрешение двух верхних уровней
a и b в каждом атоме ограничено только шириной линии Гa, но не Гa и Гb вместе (как в обычном случае). Этот феномен распространяется на путь и частотное переплетение между двумя фотонами возникающими из пространственно разделенных каскадных источников.Дальнейшее последствие двухатомной геометрии является увеличение пространственного разрешения, которое возникает поскольку фотоны запутываются в пути . То есть, пара фотонов, возникающих в разных атомах, создают интерференцию друг другу на их совместном пути. Совместное детектирование двух фотонов (каждый из длины волны
λ) показывает щелевое разрешение, которое усиливется вдвое по сравнению с классическим пределом Рэлея, λ/2. Это допускает приложения с высоким разрешением в литографии.[32-33], где удвоение разрешения является следствием того, что два фотона распространяются вдоль того же пути, и их частоты суммируются, 2ω – характеризует их совместную вероятность обнаружения. Переплетение пути не может быть имитировано распространением импульсов классического света.7. Двухдиапазонная супергетеродинная интерферометрия
Таким образом, мы рассматриваем, что двухчастичный интерферометрический эксперимент позволит нам объяснить как различные стороны фотона, считающегося надвакуумными колебаниями, так и квантовое переплетение. Мысленный эксперимент, который мы имеем в виду, основывается на фактическом эксперименте, который был выполнен с использованием параметрического низкочастотного преобразования [34]. Рассматрим установку, показанную на рисунке 7, где два атома
i = 1, 2 фиксированы в позиции и один из них выдает два фотона, помеченных фi, и γi, вызывая двухфотонное состояние, которое является суперпозицией эмиссий каждого атома:|
|
(4) |
Это запутанное состояние, в том смысле, что эмиссия фi, всегда сопровождается эмиссией
γi для i = 1 или 2. Давайте предположим, что мы заинтересованны только в интерференции фотона ф, как измерено вариацией длины пути ф1 и ф2 в детектор Dф. Фотон γ служит в качестве маркера, который потенциально записывает, какой атом выдал фотон ф. Обнаруживается, что ставя (или удаляя) заслонку на пути γ1,, интерференционные линии могут быть устранены (или появятся) в Dф, даже когда Dγ действительно не наблюден. Интересно объяснять этот феномен, используя стохастическую электродинамику [35] (как было сделано в случае Лэмбовского сдвига).Давайте заменим два фотона ф и
γ классическими полями света![]()
Это количество стремится к нулю если две фазы статистически зависимы, причиной чего является наличие заслонки между атомами. Таким образом, мы имеем здесь связь между физикой вакуумных флюктуаций (которая ответственна за спонтанную эмиссию фотонов), и физикой двухчастичных корреляций (которая явлется ключом к квантовому стирателю).
Обзор квантовой теории поля
Квантовая теория излучения [2-5] необходима для понимания обнаруженных свойств света, о которых мы упоминали выше. Центральной для теории является идея квантования поля, которая разрабатывает формальную аналогию с квантовой механикой гармонического осциллятора. Позиция
q и импульс p колеблющейся частицы удовлетворяют коммутативному отношению переключения [|
ΔEΔB |
(5) |
Такие колебания поля являются собственной характеристикой квантовой теории. Соотношение неопределенности может также формулироваться с точки зрения внутрифазовых (Eр) и внутриквадратурных (E
q) компонент электрического поля, где E(t)=EP cos vt+Eq sin vt. Для введения понятие фотона удобно привести вышеуказанное квантование поля с точки зрения декомпозиции Фурье, или с точки зрения нормальных мод поля в полости. Они соответствуют положительной частоте (идущей подобно|
E (r, |
(6) |
здесь
αk - амплитуда осцилляции, и Ek (r) - функция моды как exp(ik • r) для бегущих волн в свободном пространстве и sin(k • r) для стоячих волн в полости. Рассмотрим амплитуды осциллятораЭто естественно ведет к дискретным энергиям для поля излучения в каждой моде:
nk = 0,1,2, и т.п.. Как волны, так и частицы присутствуют в квантовом подходе, пребывая форме стохастического электромагнитного поля, послнеднее - на языке создания и уничтожения частиц. Объединение этих точек зрения в одну может представлять "фотон" как дискретное возбуждение набора мод {k} электромагнитного поля в некоторой полости, где операторы мод удовлетворяют коммутативному отношению бозонов:![]() = 1.
= 1.
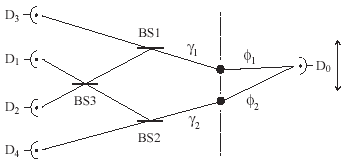
Рис. 6.
Квантовый стиратель – один из двух атомов (твердотельных схем) выдает два фотона ¢i и γi. . Интерференция наблюдается в ¢ сканирующим детектором D0. Лучевые делители BS1-BS3 направляют γ в четыре детектора. Срабатывание в детекторах D3 или D4 дает информацию о пути γ,, до интерференции в ¢.. Щелчок в детекторах DI или D2 стирает информацию о пути и вос-становливает интерференцию в ¢.. Рисунок взят из [29].Что такое фотон и где он
?Другими словами, каким способом (и на какой протяженности) мы можем говорить о фотоне, как об истиной частице, которая локализована в пространстве? Когда вначале было введено, что фотон представляется как носитель дискретных порций энергии света,
E = hv, это понятие исходило из соображений взаимодействия между излучением и веществом. Из полуклассических аргументов, мы видeли, как эта дискретность обусловлена конечными энергетическими уровнями в атоме. Здесь мы преследуем эту линию аргументации квантовой теории взаимодействия вещества - излучения, согласно которой можно полностью представить характеристику пространственной дискретности фотона, когда он взаимодействует с конечномерным атом. Эта линия мышления происходит из квантовой теории фотодетектирования [36] (которая случайно имеет отношение и к фотоэлектрическому эффекту). Тесное отношение к проблеме локализации фотона (подробно обсужденной) имеет вопрос существования фотона, как волновой функции ψ(r,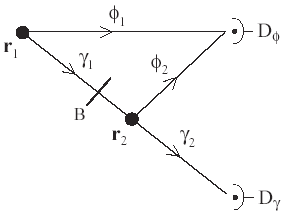
Фиг. 7.
Двухбазовая понижающая интерферометрия - Два атома располагаются в r1 и r2, один из которых выдает два фотона, помеченных как ¢i, иСвязь в том, что если такая волновая функция существует, тогда мы можем интерпретировать
Так еж как к постановке вопроса "где фотон?", одним из часто задаваемых вопросов во введении квантовой механики является: "Как единственная частица может пройти через обе щели в эксперименте Юнга?"
Ричард Фейнман отвечает на это говоря, что "никто этого не знает, и лучше всего, если Вы не будете пытаться думать об этом.
"Это хороший совет, если у вас есть картина единственного фотона как частицы. С другой стороны, если Вы обдумываете фотон как ничто другое, нежели единственное квантовое возбуждение соответствующей нормальной моды, тогда эта вещь не столь загадочна, и в некотором смысле интуитивно очевидна.
Что мы имеем в виду (взгляните на фиг.1), когда рассматриваем большой ящик, имеющий простые нормальные моды и проделанные в нем два отверстия, связанные с щелями Юнга? Если свет является параллельным в щелях, мы будем иметь на дальней стенке ящика интерференционные характеристики типа классической волновой интерференции, какие мы можем описать, как наложение нормальных мод. Сейчас мы квантуем эти нормальные моды и находим, что фотодетектор на дальней стенке будет конечно отвечать на отдельный квант возбуждения набора нормальных мод, которые локализованы в пиках интерференционной картины, и не будет отвечать, когда он расположен в узлах
.В этом смысле картина неделима. Фотон - общий для ящика и независимо тождественен при прохождении через одно или другое отверстие.
Однако для подолжения дискуссии, позвольте спросить, что же это такое, на что отвечает фотодетектор? Как мы разъясним ниже, это по существу то, что называется волновой функцией фотона [2]. Исторически сложившаяся аргументация фотона игнорировать существование этой функции. Например, в своей книге по квантовой механике [37] Хендрик Крамерс спрашивает: "Разве можно рассматривать, что уравнения Максвелла являются частным типом уравнений Шрёдингера для частиц света
?"Его предубеждение против этого взгляда основывается на различии математической формы двух типов уравнений (особенно, степени производных по времени в каждом). Первое допускает реальные решения (sin(vt) и cos(vt)) для электрических и магнитных волн, тогда как последнее ограничивается сложными волновыми функциями (
eivt и e-ivt, но не обе). Другой аргумент упоминается Дэвидом Бомом в его квантовой теории [38], где он доказывает, что нет количественного эквивалента света электронной стохастической плотности P(x) =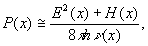
но если этот регион определен слишком хорошо, то
v(x) не имеет смысла.Бом продолжает доказывать, что уравнение непрерывности, которое связывает стохастическую плотность и текущую плотность электрона, не может быть записано для света. То есть, точное утверждение сохранения вероятности не может быть сделано для фотона. Ниже, мы увидим как мы могли бы частично ответить на возражения Крамерса и Бома.
Давайте разработаем аналогию с электроном немного дальше. Возвратимся к тому, что волновая функция электрона в координатном представлении дается
ψ(r,t) =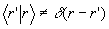
на шкале длины волны фотона. Тем не менее, мы можем все еще определить обнаружение фотона с точностью, ограниченной только размерами атома (или детектора) поглощающего его, который может в принципе быть значительно меньше, чем длина волны. Это дает точное, действующее значение в понятие "локализации" фотона в пространстве.
Если мы обнаруживаем фотон процессом поглощения, тогда взаимодействие, связывающее поле и детектор, описаны оператором уничтожения
Ệ+(r,t), определенном в уравнении (6). Согласно Золотому Правилу Ферми, матричный элемент этого оператора между начальным и конечным состояниями поля определяется как вероятность перехода. Если есть только один фотон первоначально в состоянии |i/a), тогда важным конечным состоянием является состояние вакуума |0). Стохастическая плотность обнаружения этого фотона в позиции r и времени t - таким образом пропорционально [2]|
|
(7) |
Здесь,
k - размерная константа как|
Фотон |
Нейтрино | |
|
Эйконическая физика |
Лучевая оптика (Ферма) : δ∫nds = 0 |
Классическая механика (Гамильтон): δ∫Ldt = 0 |
|
"Волновая" механика |
Уравнения Максвелла:
|
Уравнения Дирака:
|
|
Квантовая теория поля |
׀Ψ› = - |
|
Фиг. 8.
Сравнение физических теорий фотона и нейтрино. Эйконическая физика описывает их как в терминах частицы, так и параллельно с принципом Ферма в оптике и принципом Гамильтона в классической механике (L - Лагранжиан). Уравнения Tl Максвелла могут формулироваться с точки зрения волновых функций фотона, в той же форме, что и дискретные уравнения Дирака для релятивистской волновой механики нейтрино. Здесь ψ шестивекторное представление волновой функции связанной с tl электрическим и магнитным полями, p = ( (ħ / і)Δ - обычное, и s = (sx,sy,sz) набор 3 матриц x 3, который заменяет матрицы По σx, σy и σz. Смотри [2] относительно деталей. Наконец, квантовая теория поля дает унифицированное описание обоих частиц – фотонов и нейтрино с точки зрения операторов квантованного поля.
То есть, суммированием по бесконечно большому количеству волновых векторов в ур-нии (6), и обращаясь к теореме Фурье,
Ê- (r,t) может быть проинтерпретировано как оператор, который создает фотон в позиции r из вакуума. Конечно, мы должны быть осторожными , чтобы не брать эту интерпретацию слишком точно.Интересно вычислить
ψE (r,t) для фотона спонтанно выданного атомом, когда он релаксирует. Рассмотрим двухуровневый атом, расположенный в r0 , первоначально возбужденный на уровне a и релаксирующий со скоростью Г на уровень b, как показано на рисунке 2. Состояние излучаемого поля |ψ) является наложением однофотонного состояния |lk), суммированного по всем модам k, записывается как|
|
(8) |
где ω - атомная частота, и
gab,k.. - константа связи, которая зависит от дипольного момента между уровнями a и b. Спектр излученного поля - приблизительно лоренцев, который соответствует временному интервалу экспоненциальной релаксации возбужденного атома. Расчет ψE (r,t) для этого состояния, мы получаем такой|
ψE(r,t)= |
(9) |
где K - константа нормализации, r - радиальное расстояние от атома, и η - азимутальный угол атомного дипольного момента. Шаговая функция
θ (t — r/c) признак того, что ничего не будет обнаружено, пока свет от атома достигнет детектора, двигаясь со скоростью c. Как только детектор начнет видеть импульс, вероятность обнаружения |ψE|2 падает экспоненциально за время порядка Γ. Пространственный профиль импульса имитирует вид излучения классического диполя.Для какой протяженности мы можем проинтерпретировать ур-ние (9) как тип волновой функции для излученного фотона? У него несомненно есть близкая параллель с теорией Максвелла, поскольку это согласуется с тем, что мы должны зарегистрировать для электрического поля в дальней зоне излучения диполя. Мы можем пойти даже дальше и ввести векторные волновые функции
ψE и ψH, соответствующие векторам электрического и магнитного поля E и H соответственно, и показать, что они удовлетворяют уравнениям Максвелла (см. рис. 8).Этот формализм обеспечивает так называемую "потерю связи" между классической электродинамикой Максвелла и квантовой теорией поля [7]. Однако, мы должны быть осторожными в аналогиях с механикой. Например, есть реальный позиционный оператор для фотона в волново-механическом пределе, так же как для первоначально квантованного электрона. Тем не менее, волновая функция
ψE(r, t) превышает основное выражение Крамерса (так как это комплекс) и частично превышает то же самое Бома (фотодетектирование события на самом деле локализуются на расстоянии меньше длины волны). Реальная выгода вводимой волновой функции фотона получается тогда, когда мы обобщаем это количество на два или больше фотонов.Двухфотонная функция Ψ
E (r1,t1;r2,t2) может быть введена также как показано выше и использована для решения проблемы интерферометрии второго порядка (см. [2], глава 21). Переплетение между двумя фотонами ведет к неразделимости волновой функции: ΨE (r1,t1;r2,t2) ≠ ΨE (r1,t1)γE( r2,t2), так же как в примере двухфотонного состояния в ур-нии (4). Эффекты новых интерференционных эффектов, связанных с такими состояниями, могут быть объяснены в терминах этого формализма.Таким образом, концепция фотонной волновой функции полезна для сравнения интерференции классического и квантового света, и дает нам освоиться в ключевом различии между двумя парадигмами. В особенности, через асоциацию с амплитудами фотодетектирования, мультифотонными волновыми функциями свзанными с феноменологией квантово-коррелированных измерений, которые являются ключем к объяснению физики запутанного (переплетенного) света.
Выводы
Что такое фотон? В этой статье, мы старались рассматривать это понятие в однозначных терминах, оставляя его истиную чудесную и многоликую природу. История нашего путешествия в поисках понимания свойств света является на самом деле незаконченной, и идет вровень с быстрым прогрессом физической теории. Двойная концепция света, представляющая его как волну и частицу, имеет древнюю историю. Квантовая механика официально утвердила эту двойственность и устанавливает оба понятия в равной степени (вспомните квантовый стиратель). Квантовая теория света вводит вакуумные колебания в излучающее поле, и придает полям квантовые свойства, многочастичную корреляцию. Все эти развития теории дают нам свежий взгляд на вопрос о фотоне и позволяют нам прояснить нам перспективу в корпускулярно-волновой дискуссии.
Корпускулярная природа фотона очевидна в своей тенденции быть поглощенным и выделенным веществом дискретными порциями, ведет к квантованию энергии света. В пространственной области, локализация фотонов фотодетектором делает возможным то, чтобы определить “волновую функцию” для фотона, которая предоставляет “сначала”, квантованный вид электромагнитного поля аналогичный квантовой механике материальных частиц. Квантовая интерференция и переплетение описывают одино- и двухфотонные волновые функции, что облегчает их сравнение для объяснения в рамках классической волновой оптики. Более того, этот формализм в режиме интерпретации прокладывает мост между двумя древними, антитетическими понятиями света – локальностью частицы и функциональным свойством волны.
Литература
перевод на русский
Карима Хайдарова, 2004