 |
|
Прочитано: 9% |
«««Назад | Первоисточник | Сны наяву | Далее»»»
 |
|
Прочитано: 9% |
Наши
современные представления о законах движения тел восходят к Галилею и Ньютону.
До них бытовала точка зрения Аристотеля, который считал, что естественным
состоянием любого тела является состояние покоя и тело начинает двигаться только
под действием силы или импульса. Отсюда следовало, что тяжелое тело должно
падать быстрее, чем легкое, потому что его сильнее тянет к земле.
Согласно
аристотелевской традиции, все законы, которые управляют Вселенной, можно вывести
чисто умозрительно и нет никакой необходимости проверять их на опыте. Поэтому до
Галилея никто не задумывался над тем, действительно ли тела разного веса падают
с разными скоростями. Говорят, что
Галилей демонстрировал
ложность учения Аристотеля, бросая тела разного веса с падающей Пизанской башни.
Это наверняка выдумка, но Галилей действительно делал нечто подобное: он
скатывал по гладкому откосу шары разного веса. Такой эксперимент аналогичен
сбрасыванию тяжелых тел с башни, но он проще для наблюдений, так как меньше
скорости. Измерения Галилея показали, что скорость всякого тела увеличивается по
одному и тому же закону независимо от веса тела. Например, если взять шар и
пустить его вниз по наклонной плоскости с уклоном метр на каждые десять метров,
то, каким бы тяжелым ни был шар, его скорость в конце первой секунды будет один
метр в секунду, в конце второй секунды - два метра в секунду и т. д. Конечно,
свинцовая гиря будет падать быстрее, чем перышко, но только из-за того, что перо
сильнее замедляется силой сопротивления воздуха, чем гиря. Если бросить два
тела, сопротивление воздуха для которых невелико, например две свинцовые гири
разного веса, то они будут падать с одинаковой скоростью.
Ньютон вывел свои
законы движения, исходя из измерений, проведенных Галилеем. В экспериментах
Галилея на тело, катящееся по наклонной плоскости, всегда действовала одна и та
же сила (вес тела) и в результате скорость тела постоянно возрастала. Отсюда
следовало, что в действительности приложенная к телу сила изменяет скорость
тела, а не просто заставляет его двигаться, как думали раньше. Это еще означало,
что если на тело не действует сила, оно будет двигаться по прямой с постоянной
скоростью. Такую мысль впервые четко высказал Ньютон в своей книге
"Математические начала", вышедшей в 1687 г. Этот закон теперь называется Первым
законом Ньютона. О том, что происходит с телом, когда па него действует сила,
говорится во Втором законе Ньютона. Он гласит, что тело будет ускоряться, т. е.
менять свою скорость, пропорционально величине силы. (Если, например, сила
возрастет в 2 раза, то и ускорение в 2 раза увеличится). Кроме того, ускорение
тем меньше, чем больше масса (т. е. количество вещества) тела. (Действуя на тело
вдвое большей массы, та же сила создает вдвое меньшее ускорение). Всем хорошо
известно, как обстоит дело с автомобилем: чем мощнее двигатель, тем больше
создаваемое им ускорение, но чем тяжелее автомобиль, тем меньше ускоряет его тот
же двигатель.
Кроме
законов движения Ньютон открыл закон, которому подчиняется сила тяготения. Этот
закон таков: всякое тело притягивает любое другое тело с силой, пропорциональной
массам этих тел. Следовательно, если вдвое увеличить массу одного из тел
(скажем, тела А), то и сила, действующая между телами, тоже увеличится в 2 раза.
Мы так считаем потому, что новое тело А можно представить себе составленным из
двух тел, масса каждого из которых равна первоначальной массе. Каждое из этих
тел притягивало бы тело В с силой, равной первоначальной силе. Следовательно,
суммарная сила, действующая между телами А и В, была бы вдвое больше этой
первоначальной силы. А если бы одно из тел имело массу, скажем, вдвое, а второе
- втрое больше первоначальной массы, то сила взаимодействия возросла бы в 6 раз.
Теперь понятно, почему все тела падают с одинаковой скоростью: тело с удвоенным
весом будет тянуть вниз удвоенная гравитационная сила, но и масса тела при этом
будет в 2 раза больше. По Второму закону Ньютона эти два эффекта компенсируют
друг друга, и ускорение будет во всех случаях одинаковым.
Закон тяготения
Ньютона говорит, что чем дальше тела друг от друга, тем меньше сила их
взаимодействия. Согласно этому закону, гравитационная сила притяжения звезды
составляет ровно четверть силы притяжения такой же звезды, но находящейся на
вдвое меньшем расстоянии. Закон Ньютона позволяет с большой точностью
предсказать орбиты Земли, Луны и планет. Если бы закон всемирного тяготения был
иным и сила гравитационного притяжения уменьшалась быстрее, чем по закону
Ньютона, то орбиты планет были бы не эллипсами, а спиралями, сходящимися к
Солнцу. Если же гравитационное притяжение убывало бы с расстоянием медленнее, то
притяжение удаленных звезд оказалось бы сильнее притяжения Земли.
Представления
Аристотеля существенно отличались от представлений Галилея и Ньютона тем, что
Аристотель считал состояние покоя неким предпочтительным состоянием, в котором
всегда должно оказываться тело, если на него не действует сила или импульс.
Аристотель, в частности, считал, что Земля покоится. Из законов Ньютона же
следует, что единого эталона покоя не существует. Вы можете на равных основаниях
утверждать, что тело А находится в покое, а тело В движется относительно тела А
с постоянной скоростью или же что тело В, наоборот, покоится, а тело А движется.
Если, например, забыть на время о вращении нашей планеты вокруг оси и о ее
движении вокруг Солнца, то можно сказать, что земля покоится, а поезд несется на
север со скоростью девяносто километров в час или же что поезд стоит на месте, а
земля под ним убегает на юг со скоростью 90 километров в час. Если бы в этом
поезде ктонибудь экспериментировал с движущимися телами, то оказалось бы, что
все законы Ньютона выполняются. Например, играя в поезде в настольный теннис, вы
обнаружили бы, что траектория шарика подчиняется законам Ньютона, как если бы вы
играли на неподвижном столе, и вы не могли бы сказать, что именно движется -
поезд или земля.
Отсутствие абсолютного
эталона покоя означает, что невозможно определить, произошли ли некие два
события в одной и той же точке пространства, если известно, что они имели место
в разные моменты времени. Пусть, например, наш теннисный шарик в движущемся
поезде отскакивает от стола вертикально вверх и, падая вниз, ударяется через
секунду о стол в той же точке. Тому, кто стоит у железнодорожного полотна,
показалось бы, что точки соприкосновения шарика со столом разделены расстоянием
около сорока метров, которое прошел поезд за время между подскоками.
Следовательно, отсутствие абсолютного состояния покоя означает, что никакому
событию нельзя приписать абсолютного положения в пространстве, как это полагал
Аристотель. Положение событий в пространстве и расстояния между ними должны быть
разными для наблюдателя, едущего в поезде, и для наблюдателя, который стоит
рядом с проходящим поездом, и нет никаких оснований считать, что положения,
фиксируемые одним из этих наблюдателей, более предпочтительны, чем положения,
фиксируемые другим.
Ньютона сильно
беспокоило отсутствие абсолютного положения в пространстве или, как его
называли, абсолютного пространства, потому что это противоречило его идее
абсолютного Бога. И он фактически отказался принять отсутствие абсолютного
пространства, несмотря на то что такое отсутствие вытекало из законов, открытых
им самим. Многие резко критиковали Ньютона за его иррациональное упорство, и в
частности епископ Беркли - философ, считавший, что все материальные объекты, а
также пространство и время - иллюзия. (Узнав о таких воззрениях Беркли,
знаменитый д-р Джонсон воскликнул: "Я опровергаю это вот как!" - и так стукнул
ногой по большому камню, что чуть не потерял равновесие).
И Аристотель, и Ньютон
верили в абсолютное время. Иными словами, они считали, что временной интервал
между двумя событиями можно однозначно измерить и что результат будет одинаков
независимо от того, кто производит измерения, лишь бы у измеряющего были
правильные часы. Время было полностью отделено от пространства и считалось не
зависящим от него. Такова была точка зрения большинства, точка зрения здравого
смысла. Но нам пришлось изменить свои представления о пространстве и времени.
Представления, основанные на "здравом смысле", относятся к сравнительно
медленным объектам (яблоко, планета), но они оказываются совершенно неуместными,
когда скорости становятся близкими к скорости света.
То, что свет
распространяется с конечной, хотя и очень большой скоростью, установил в 1676 г.
датский астроном Оле Христенсен Рёмер. Он обнаружил, что моменты прохождения
спутников Юпитера за его диском следуют один за другим не через равные
интервалы, как должно быть, если спутники вращаются вокруг Юпитера с постоянной
скоростью. При вращении Земли и Юпитера вокруг Солнца расстояние между этими
двумя планетами изменяется. Рёмер заметил, что затмения лун Юпитера тем больше
запаздывают, чем дальше мы от него находимся. Он объяснил это тем, что свет от
спутников идет до нас дольше, когда мы находимся дальше. Однако Рёмер не очень
точно измерял изменения расстояния от Земли до Юпитера, и поэтому полученное им
значение скорости света оказалось равным 140.000 миль/с, тогда как современное
значение составляет 186.000 миль/с (1 миля = 1,609 км. Современное значение
скорости света равно 299.792.458 м/с. - прим. перев.). Тем не менее достижение
Рёмера было выдающимся, ибо он не только доказал, что свет распространяется с
конечной скоростью, но и измерил ее, причем все это за одиннадцать лет до выхода
в свет книги Ньютона "Математические начала".
Настоящей теории
распространения света не существовало до 1865 г., когда английский физик Джеймс
Кларк Максвелл сумел объединить две частные теории, с помощью которых тогда
описывали электрические и магнитные силы. Согласно уравнениям Максвелла, в
электромагнитном поле, составленном из двух полей, могут существовать
волноподобные возмущения, которые распространяются с постоянной скоростью, как
волны на поверхности пруда. Если длина волны (т. е. расстояние между гребнями
двух соседних волн) составляет метр или больше, то мы имеем дело с радиоволнами.
Более короткие волны называются волнами сверхвысокочастотного диапазона (если их
длина - порядка сантиметра) и волнами инфракрасного диапазона (до десяти
тысячных сантиметра). Длина волны видимого света составляет всего лишь
сорок-восемьдесят миллионных долей сантиметра. Еще короче волны
ультрафиолетового, рентгеновского и гамма-излучений.
Теория Максвелла
предсказывала, что радиоволны и свет должны распространяться с некоторой
фиксированной скоростью. Но поскольку теория Ньютона покончила с представлением
об абсолютном покое, теперь, говоря о фиксированной скорости света, нужно было
указать, относительно чего измеряется эта фиксированная скорость. В связи с этим
было постулировано существование некой субстанции, названной "эфиром", которой
наполнено все, даже "пустое" пространство. Световые волны распространяются в
эфире так же, как звуковые в воздухе, и, следовательно, их скорость - это
скорость относительно эфира. Наблюдатели, с разными скоростями движущиеся
относительно эфира, должны видеть, что свет идет к ним с разной скоростью, но
скорость света относительно эфира должна оставаться при этом неизменной. В
частности, коль скоро Земля движется в эфире по своей орбите вокруг Солнца,
скорость света, измеренная в направлении движения Земли (при движении в сторону
источника света), должна превышать скорость света, измеренную под прямым углом к
направлению движения (т. е. когда мы не движемся к источнику). В 1887 г. Альберт
Майкельсон (впоследствии ставший первым американцем, удостоенным Нобелевской
премии по физике) и Эдвард Морли поставили в Кливлендской школе прикладных наук
очень точный эксперимент. Майкельсон и Морли сравнивали значение скорости света,
измеренной в направлении движения Земли, с ее значением, измеренным в
перпендикулярном направлении. К своему огромному удивлению, они обнаружили, что
оба значения совершенно одинаковы!
С 1887 по 1905 г. был
сделан ряд попыток (наиболее известная из которых принадлежит датскому физику
Хендрику Лоренцу) объяснить результат эксперимента Майкельсона и Морли тем, что
все движущиеся в эфире объекты сокращаются в размерах, а все часы замедляют свой
ход. Но в 1905 г. никому доселе не известный служащий Швейцарского патентного
бюро по имени Альберт Эйнштейн опубликовал ставшую потом знаменитой работу, в
которой было показано, что никакого эфира не нужно, если отказаться от понятия
абсолютного времени. Через несколько недель ту же точку зрения высказал один из
ведущих французских математиков Анри Пуанкаре. Аргументы, выдвинутые Эйнштейном,
были ближе к физике, чем аргументы Пуанкаре, который подошел к этой задаче как к
математической. Об Эйнштейне обычно говорят как о создателе новой теории, но и
имя Пуанкаре связывают с разработкой важной се части.
Фундаментальный
постулат этой теории относительности, как стали называть новую теорию, состоял в
том, что законы науки должны быть одинаковыми для всех свободно движущихся
наблюдателей независимо от скорости их движения. Этот постулат был справедлив
для законов движения Ньютона, но теперь он был распространен на теорию Максвелла
и на скорость света; скорость света, измеренная любыми наблюдателями, должна
быть одинакова независимо от того, с какой скоростью движутся сами наблюдатели.
Из этого простого принципа вытекает ряд замечательных следствий. Самые известные
из них - это, наверное, эквивалентность массы и энергии, нашедшая свое выражение
в знаменитом уравнении Эйнштейна Е = mc^2 (где Е - энергия, m - масса, а с -
скорость света), и закон, согласно которому ничто не может двигаться быстрее
света. В силу эквивалентности массы и энергии энергия, которой обладает
движущийся объект, должна теперь добавляться к его массе. Другими словами, чем
больше энергия, тем труднее увеличить скорость. Правда, этот эффект существенен
лишь при скоростях, близких к скорости света. Если, например, скорость
какого-нибудь объекта составляет 10% скорости света, то его масса лишь на 0,5%
больше нормальной, тогда как при скорости, равной 90% скорости света, масса уже
в 2 раза превышает нормальную. По мере того как скорость объекта приближается к
скорости света, масса растет все быстрее, так что для дальнейшего ускорения
требуется все больше и больше энергии. На самом деле скорость объекта никогда не
может достичь скорости света, так как тогда его масса стала бы бесконечно
большой, а поскольку масса эквивалентна энергии, для достижения такой скорости
потребовалась бы бесконечно большая энергия. Таким образом, любой нормальный
объект в силу принципа относительности навсегда обречен двигаться со скоростью,
не превышающей скорости света. Только свет и другие волны, не обладающие
"собственной" массой, могут двигаться со скоростью света.
Другое замечательное
следствие из постулата относительности - революция в наших представлениях о
пространстве и времени. По теории Ньютона, если световой импульс послан из одной
точки в другую, то время его прохождения, измеренное разными наблюдателями,
будет одинаковым (поскольку время абсолютно), по пройденный им путь может
оказаться разным у разных наблюдателей (так как пространство не является
абсолютным). И поскольку скорость света есть пройденное светом расстояние,
деленное на время, разные наблюдатели будут получать разные скорости света. В
теории относительности же все наблюдатели должны быть согласны в том, с какой
скоростью распространяется свет. И коль скоро у них нет согласия в вопросе о
расстоянии, пройденном светом, у них не должно быть согласия и в том, сколько
времени шел свет. (Время прохождения - это пройденное светом расстояние,
относительно которого нет согласия у наблюдателей, деленное на скорость света,
относительно которой все согласны). Иными словами, теория относительности
покончила с понятием абсолютного времени! Оказалось, что у каждого наблюдателя
должен быть свой масштаб времени, измеряемого с помощью имеющихся у него часов,
и что показания одинаковых часов, находящихся у разных наблюдателей, не
обязательно согласуются.
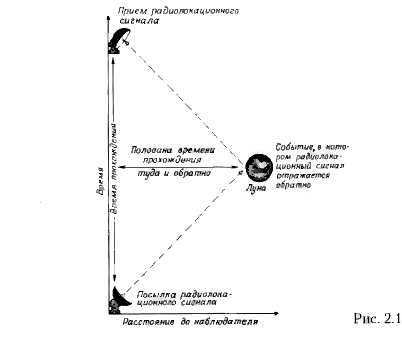
Всякий
наблюдатель может определить, где и когда произошло какое-нибудь событие,
методом радиолокации, послав световой импульс или импульс радиоизлучения. Часть
посланного сигнала в конце пути отразится назад, и наблюдатель измерит время
возврата эхо-сигнала. Временем события будет середина интервала между посылкой
сигнала и его возвращением: расстояние до события равно половине времени,
затраченного на прохождение туда и обратно, умноженной на скорость света. (Под
событием здесь понимается нечто, происходящее в определенной точке пространства
в определенный момент времени). Все сказанное поясняется
пространственновременной диаграммой, представленной на рис. 2.1. При изложенном
методе наблюдатели, перемещающиеся относительно друг друга, припишут одному и
тому же событию разное время и положение в пространстве. Ни одно из измерений,
произведенных разными наблюдателями, не будет правильнее других, но все они
будут связаны между собой. Каждый наблюдатель может точно вычислить, какое время
и какое положение в пространстве припишет событию любой другой наблюдатель, если
известна скорость второго наблюдателя относительно первого.
Для точного
определения расстояний сейчас пользуются именно таким методом, потому что время
мы умеем измерять точнее, чем длину. Даже метр определяется как расстояние,
которое свет проходит за время 0,000000003335640952 секунды, измеренное при
помощи цезиевых часов. (Само это число соответствует историческому определению
метра как расстояния между двумя отметками на специальном платиновом стержне,
хранящемся в Париже). Мы можем пользоваться и более удобной новой единицей
длины, которая называется световой секундой. Это просто расстояние, которое свет
проходит за одну секунду. В теории относительности расстояние теперь определено
через время и скорость света, откуда автоматически следует, что, измеряя
скорость света, каждый наблюдатель получит один и тот же результат (по
определению 1 метр за 0,000000003335640952 секунды). Теперь не нужно вводить
эфир, присутствие которого, кстати, как показал опыт Майкельсона-Морли, и
невозможно обнаружить. Однако теория относительности вынуждает нас к
фундаментальной смене представлений о пространстве и времени. Нам приходится
принять, что время не отделено полностью от пространства и не независимо от
него, но вместе с ним образует единый объект, который называется
пространством-временем.
Из повседневного опыта
мы знаем, что положение точки в пространстве можно задать тремя числами - ее
координатами. Можно, например, сказать, что некая точка в комнате находится в
двух метрах от одной стены, в метре - от другой и в полутора метрах от пола. А
можно также задать ее положение, указав широту, долготу и высоту над уровнем
моря. Вы можете пользоваться любыми тремя подходящими координатами, хотя они
всегда имеют лишь ограниченную область применимости. Никто не станет, задавая
положение Луны, указывать расстояние в километрах на север и на запад от площади
Пикадилли и высоту над уровнем моря. Вместо этого можно указать расстояние до
Солнца, расстояние до плоскости, в которой лежат орбиты планет, и угол между
прямой, соединяющей Луну с Солнцем, и прямой, соединяющей Солнце с какой-нибудь
близкой звездой, скажем, с альфой Центавра. Правда, и эти координаты вряд ли
подходят для задания положения Солнца в нашей Галактике или положения нашей
Галактики среди окружающих нас других галактик. Но можно всю Вселенную разбить
на перекрывающиеся "куски" и для каждого "куска" ввести свою систему координат,
чтобы задавать в нем положение точки.