Эффект Казимира
Эффект Казимира: сила "из ничего"
Астрид Ламбрехт (Astrid Lambrecht)
перевод Павлюченко С.
Сила притяжения между двумя поверхностями в вакууме, впервые предсказанная Генрихом Казимиром (Hendrik Casimir) более 50 лет назад, может повлиять практически на все - от микроприборов до теорий Мироздания.
Что произойдет если Вы возьмете два зеркала и
установите их зеркальными сторонами друг к другу в пустом
пространстве ? Да ничего не произойдет, скажете Вы. А на самом деле
зеркала притягиваются друг к другу из-за того, что между ними
находится вакуум. Это явление было впервые предсказано немецким
физиком-теоретиком Генрихом Казимиром в 1948 году, когда он работал
в исследовательском центре Philips Research Laboratories в
Эйндховене (Eindhoven) над коллоидными растворами (см.
Долгие годы эффект Казимира был не многим более, чем интересной теорией. Но в последние годы интерес к этому явлению вырос. Физики-экспериментаторы обнаружили, что сила Казимира оказывает влияние на микромеханизмы, а прогресс в техническом оснащении сделал возможным измерение этой силы со значительно большей точностью.
Интересен этот эффект и с точки зрения фундаментальной физики. Многие теории предсказывают существование "протяженных" дополнительных измерений в 10- и 11-мерных теориях. Согласно этим теориям, должно наблюдаться отклонение от классической ньютоновой гравитации на субмиллиметровых расстояниях. Измерения действия эффекта Казимира таким образом может помочь в проверке подобных гипотез.
| Казимир и коллоидные растворы |
| Тот факт, что между двумя проводящими пластинами будет
существовать сила притяжения, был предсказан в 1948 году
Генрихом Казимиром из Philips Research Laboratories в
Нидерландах. В то время Казимир изучал свойства коллоидных
растворов. Это вязкие вещества, такие, как краска или майонез,
имеющие в своем составе частички микронных размеров. Свойства
таких растворов определяются Ван-дер-Ваальсовыми силами -
дальнодействующими силами притяжения между нейтральными
атомами и молекулами.
Один из коллег Казимира, Тео Овербек (Theo Overbeek), обнаружил, что теория, используемая для объяснения Ван-дер-Ваальсовых сил, развитая Фрицом Лондоном (Fritz London) в 1932 году, не может адекватно объяснить данные экспериментов. После этого Овербек попросил Казимира исследовать эту проблему. Работая вместе с Дирком Полдером (Dirk Polder), Казимир открыл, что взаимодействие между двумя нейтральными молекулами не может быть правильно описано исходя только из постоянства скорости света. Вскоре Казимир заметил, что этот результат может быть описан, если принять во внимание флуктуации вакуума. Он спросил себя, что будет, если бы вместо двух молекул были бы два зеркала, повернутые отражаюшими сторонами друг к другу. Этот вопрос и привел его к знаменитому предсказанию о притягвающей силе, существующей между отражающими пластинами. |
Что такое сила Казимира ?
Хотя сила Казимира и кажется полностью противоестественной, ее можно понять. Во времена классической механики представление о вакууме было простым. Под вакуумом понимался "резервуар" всевозможных частиц, находящихся при низких температурах вплоть до абсолютного нуля. С приходом квантовой механики наше мнение о вакууме кардинально изменилось. Все поля - электромагнитное, в частности, - флуктуируют. Иными словами, их значение в каждый момент времени не равно константе (среднему значению), а "колеблется" вблизи него. Даже для "истинного" вакуума вблизи абсолютного нуля известны так называемые "вакуумные флуктуации" со средней энергией, равной половине энергии фотона (это для случая электромагнитного поля).
Может показаться, что флуктуации вакуума это некоторые абстракции, возникшие в больном мозгу физика, но это не так. Их наблюдаемые проявления вполне могут быть экспериментально обнаружены в микромире. Например, атом не будет оставаться бесконечно долго в возбужденном состоянии, а перейдет в основное, спонтанно испустив фотон. Это явление - следствие флуктуаций вакуума. Попробуйте удержать карандаш "прямостоящим" на конце пальца. Он будет стоять, но только если Ваша рука будет абсолютно устойчивой и ничто не будет нарушать равновесия карандаша. Но малейшее колебание повергнет карандаш в более устойчивое равновесное состояние. Так и атом в возбужденном состоянии - под действием флуктуаций вакуума он переходит в свое основное состояние.
 |
Сила Казимира - наиболее известное механическое проявление
флуктуаций вакуума. Рассмотрим щель между двумя плоскими зеркалами
как потенциальную яму (
При обсуждении силы Казимира нельзя не упомянуть о "давлении поля излучения". Каждое поле - даже вакуум - переносит энергию. Электромагнитные поля не просто распостраняются в пространстве - они еще и оказывают давление на поверхности, так же, как вода давит на плотину. Давление излучения растет с ростом энергии и, таким образом, с частотой электромагнитного поля. Давление излучения на резонансных частотах внутри полости сильнее, чем снаружи и зеркала отталкиваются. Вне резонанса же наоборот - давление внутри меньше, чем снаружи и зеркала притягиваются друг к другу. Так как отталкивание происходит на конкретном наборе частот, а притягивание - на всех остальных частотах, то притягивающая компонента все же "сильнее" отталкивающей. При этом необходимо отметить, что обе компоненты - как притягивающая, так и отталкивающая - существуют одновременно.
Итак, два идеальных плоских параллелных зеркала благодаря эффекту
Казимира притягиваются друг к другу. Возникающая при этом сила, ![]() , пропорциональна площади общей части зеркал
, пропорциональна площади общей части зеркал
![]() и обратно пропорциональна 4-й степени
расстояния между зеркалами:
и обратно пропорциональна 4-й степени
расстояния между зеркалами: ![]() . Кроме этих геометрических величин, сила
зависит только от фундаментальных констант - постоянной Планка и
скорости света.
. Кроме этих геометрических величин, сила
зависит только от фундаментальных констант - постоянной Планка и
скорости света.
Так как сила Казимира очень слаба, ее можно обнаружить, только
если зеркала разнесены на несколько микрон (а не несколько метров).
Например, два зеркала с площадями ![]() , разделенные расстоянием в 1 микрон,
притягиваются с силой в
, разделенные расстоянием в 1 микрон,
притягиваются с силой в ![]() ньютонов - это вес капли воды диаметром в
полмиллиметра. Хотя эта сила и кажется маленькой, на расстояниях
меньше микрона она сильно растет и оказывается сравнимой с
природными силами. На расстояниях порядка 10 нм - сотни размеров
типичного атома - давление, создаваемое эффектом Казимира,
оказывается сравнимым с атмосферным.
ньютонов - это вес капли воды диаметром в
полмиллиметра. Хотя эта сила и кажется маленькой, на расстояниях
меньше микрона она сильно растет и оказывается сравнимой с
природными силами. На расстояниях порядка 10 нм - сотни размеров
типичного атома - давление, создаваемое эффектом Казимира,
оказывается сравнимым с атмосферным.
Хотя в посведневной жизни мы и не имеем дел с таким малыми расстояниями, они важны в нанотехнологиях и микроэлектромеханических системах (МЭМС). Это "умные" приборы микронных размеров, в которых механические и движущие элементы, такие, как крохотные сенсоры и микродвигатели, вырезаны на кремниевой подложке. Применяются они в науке и инженерии, например, как измерители давления в автомобилях.
 |
Так как элементы МЭМС'ов выполнены на микронном и субмикронном
уровнях, сила Казимира может заставить крошечные элементы в этих
устройствах "слипнуться" - заявил недавно Майкл Рукс (Michael
Roukes) с сотрудниками из Калифорнийского Технологического Института
(2001 Phys. Rev. B 63 033402). Но она может сослужить
и хорошую службу. В прошлом году Федерико Капассо (Federico Capasso)
и его группа из Lucent Technologies показали, как ее можно
использовать для контроля движения МЭМС'а (2001 Science
291 1941). Исследователи подвесили полисиликоновую пластину
на вращающийся стержень - цилиндрический брусочек диаметром всего
несколько миллиметров (
Измерение эффекта Казимира
Эффект Казимира был предсказан, как уже указывалось ранее, в 1948 году, но открыть его экспериментально, пользуясь технологиями того времени, было очень трудно. Один из первых экспериментов был проведен в 1958 году Маркусом Спаарней (Marcus Spaarnay) из центра Philips в Эйндховене, который иследовал силу Казимира, возникающую между двуми плоскими металлическими зеркалами, сделанными из аллюминия, хрома или стали. Спаарней измерил силу, используя равновесие пружинки, растяжение которой определяло объем, заключенный между пластинками. Для того, чтобы сила Казимира была не была принята за электростатическую, зеркала удерживают нейтральными. Также Спаарней обеспечивал строгую параллельность плоскостей зеркал, так как сила Казимира очень чуствительна к расстоянию. Спаарней преодолел эти трудности и заключил, что его результаты "не противоречат теоретическим предсказаниям Казимира".
С тех пор, однако, более точное оборудование значительно упростило изучение эффекта Казимира. Новое поколение экспериментов началось в 1997 году. Стив Ламоро (Steve Lamoreaux) из Университета Вашингтона в Сиэтле измерил эффект Казимира между сферической линзой диаметром 4 см и кварцевой пластиной 2.5 см в поперечнике, покрытыми медью и золотом. Линза и пластина были соединены с маятником - изогнутым горизонтальным брусоком, подвешенным на вольфрамовой проволоке, помещенным в цилиндрический сосуд в вакууме. Когда Ламоро поместил линзу и пластину на расстояниии нескольких микрон, сила Казимира соединила оба объекта вместе и заставила маятник вращаться. В его опытах согласие эксперимента с теорией наблюдалось на уровне 95% .
 |
Воодушевленные прорывом Ламоро, многие другие исследователи
начали ставить новые эксперименты по измерению эффектов силы
Казимира. Например, Умар Мохиден с сотрудниками из Калифорнийского
Университета в Риверсайде (Riverside) прикрепили полистиреновую
сферу 200 микрон в диаметре к наконечнику атомного микроскопа (
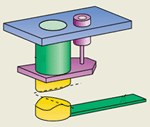 |
Томас Эдет (Thomas Ederth) из Королевского Технологического
Института (Royal Institute of Technology) в Стокгольме, Швеция,
также использовал атомный микроскоп для изучения эффекта Казимира.
Он измерил силу, возникающую между двумя цилиндрами, покрытыми
золотом, повернутыми на 90° друг относительно друга и разделенными
расстоянием в 20 нанометров. Его результат согласуется с теорией
лучше, чем на 99% (
Однако, очень не во многих экспериментах, измеряющих силу Казимира, использовалась оригинальная конфигурация плоскостей как параллельных зеркал. Связано это с тем, что их необходимо сохранять параллельными в течение всего эксперимента, что очень тяжело. Значительно проще поднести сферу достаточно близко к зеркалу, так как расстояние между объектами, используемое в формуле для вычисления силы, в данном случае - просто расстояние между ближайшими точками. Единственный недостаток использования сферы и плоского зеркала состоит в том, что вычисления силы Казимира в этом случае не так точны, как в случае двух параллельных зеркал. В частности, предполагается, что вклады силы между сферой и пластиной полностью независимы в каждой точке. А это верно только если радиус сферы много больше расстояния между сферой и пластиной.
И лишь совсем недавно был проведен эксперимент, полностью повторяюший Казимировскую систему из двух плоских, параллельных зеркал. Он был проведен Джанни Каругно (Gianni Carugno), Роберто Онофрио (Roberto Onofrio) с сотрудниками из Университета Падовы в Италии. Они измерили силу между жесткой хромированной пластинкой и плоской поверхностью кронштейна, сделанного из такого же материала, которые были разнесены на 0.5-3 микрона (G Bressi et al. 2002 Phys. Rev. Lett. 88 041804). По их измерениям, сила Казимира согласуется с теоретическим предсказанием на 75 % . Такая относительно большая погрешность связана с техническими трудностями при осуществлении эксперимента.
Более точные вычисления
Проблема в изучении эффекта Казимира состоит в том, что обычные зеркала - не идеально гладкие и плоские, как рассматривал Генрих Казимир. В частности, обычные зеркала не отражают идеально на всех длинах волн. На некоторых они отражают хорошо - даже почти идеально, в то же время как на других - плохо. Кроме того, все зеркала становятся прозрачными на очень высоких частотах. Таким образом, при вычислении силы Казимира необходимо принимать во внимание зависящие от частот коэффициенты отражения от зеркал. Эту проблему рассматривал Евгений Лифшиц в 1950-е годы, потом Джулиан Швингер (Julian Schwinge) и многие другие.
Оказалось, что измеряемая сила Казимира между обычными металлическими зеркалами, находящимися на расстоянии 0.1 микрон, составляет только половину от предсказываемой теорией для идеальных зеркал. Если не принимать во внимание это разногласие при сравнении экспериментальных данных с теорией, можно сделать неверное заключение о том, что это несогласие вызвано существованием новой силы. Астрид Ламбрехт (Astrid Lambrecht) и его коллега Серж Рейнод (Serge Reynaud) проводили свои вычисления для реального поведения зеркал, принимая во внимание физические свойства металлов. Они заключили, что в случае простейшей модели зеркала ведут себя "нормально" на расстояниях, превышающих 0.5 микрон.
Другой прблемой, возникающей при вычислении теоретического значения силы Казимира, является тот факт, что эксперимент в принципе не может быть проведен при абсолютном нуле - что предполагалось в вычислениях Казимира - а проводится при комнатной температуре. Из-за этого приходится учитывать еще и тепловые флуктуации. Они могут создать собственное давление излучения и этим увеличить эффект силы Казимира. Например, сила Казимира, действующая между плоскими зеркалами, разнесенными на 7 микрон, при комнатной температуре оказывается в два раза больше, чем при абсолютном нуле. К счастью, тепловые флуктуации при комнатной температуре важны лишь на дистанциях больше одного микрона, при меньших расстояниях длина волны флуктуации слишком велика, чтобы хотя бы один раз полностью уложиться в потенциальную яму.
Хотя влияние температуры на силу Казимира еще не исследовано в деталях, ее необходимо учитывать при расстояниях, превышающих один микрон. Многие исследователи бились над этой проблемой, в том числе Лифшиц и Швингер в 1950-х. Не так давно ее рассматривали Майкл Бордаг (Michael Bordag) из Университета Лейпцига, Бо Сернелиус (Bo Sernelius) из Университета Линкопинг (Linköping University) в Швеции, Галина Климчитская и Владимир Мостапенко из Университета Парайбы (University of Paraiba) а Бразилии, а также группа Астрида Ламбрехта в Париже. Зависимость силы Казимира от температуры была некоторое время назад темой горячих обсуждений в научной среде. Правда, многие противоречия уже разрешены, но они стимулировали эксперименты по определению зависимости силы Казимира от температуры.
Третьей и последней проблемой при вычислении силы Казимира является тот факт, что настоящие зеркала не идеально гладкие. Подавляющее большинство зеркал сделаны путем покрытия основы тонкой металлической пленкой; при этом используется технология "напыления". В этом случае толщина пленки колеблется на 50 нм. Такая точность незаметна для невооруженного глаза, но оказывает влияние на измеряемое значение силы Казимира, которая очень чуствительна к расстоянию.
Мохиден (Mohideen) и его группа (Калифорния), используя деформированные поверхности, недавно показали, что такие поверхности также испытывают "боковую" силу Казимира, которая действует не в перпендикулярном, а в параллельном направлении по отношению к зеркалу. Для экспериментов они приготовили специальные зеркала, поверхности которых были синусоидально искривлены. Затем они двигали зеркала таким образом, чтобы пик одного из зеркал проходил последовательно через пики и "минимумы" второго зеркала. Было обнаружено, что боковая сила Казимира меняется синусоидально с разностью фаз между двумя "волнами". Величина силы оказалась в 10 раз меньше, чем она была бы в случае "нормальных" зеркал, разнесенных на такое же расстояние. Боковая сила своей природой также обязана флуктуациям вакуума.
Мехран Кадар (Mehran Kadar) с сотрудниками из Массачусетского Технологического Института вычислили теоретическое значение силы между двумя идеально отражаюшими волнистыми зеркалами, в то время как Мохиден с коллегами пересчитали ее для металлических зеркал и нашли хорошее согласие теории с экспериментом. Боковая сила Казимира может иметь и другие последствия для микроприборов.
Новая физика ?
Эффект Казимира может также играть роль при точных измерениях силы в микромире на микро- и нанометровых шкалах. Ньютоновский закон много раз проверялся в макромире, например, при исследовании движения планет. Но еще никому не удавалось проверить его на микронных расстояниях с хорошей точностью. Такие тесты очень важны, так как существует множество теорий, в которых происходит объединение всех четырех взаимодействий, и эти теории предсказывают существование новых сил, действующих на этих шкалах. Таким образом, любое расхождение между экспериментом и теорией может интерпретироваться как существование новых сил. В любом случае, измерения положат новые ограничения на существуюшие теории.
Джинс Гандблах (Jens Gundlach) с коллегами из Вашингтона, например, использовали крутильный маятник для определения гравитационной силы между двумя тестовыми массами, разделенными от 10 мм до 220 микрон. Их измерения подтвердили, что ньютоновская гравитация действует на этих шкалах, а сила Казимира доминирует на значительно меньших расстояниях. Тем временем Джошуа Лонг (Joshua Long), Джонн Прайс (John Price) с коллегами из Университета Колорадо вместе с Эфрамом Фишбахом (Ephraim Fischbach) и его сотрудниками из Университета Парду (Purdue University) попытались устранить действие эффекта Казимира на субмиллиметровые тесты гравитации путем более тщательного выбора материалов, используемых в эксперименте.
Эта статья дает только краткий обзор многих экспериментальных и теоретических исследований эффекта Казимира. Конечно, существует множество не менее захватывающих экспериментов. Многие научные группы, например, изучают, что будет, если во взаимодействии между зеркалами участвует не электромагнитное поле, переносчиком которого являются безмассовые бозоны, а поля массивных фермионов, таких, как кварки или нейтрино. Другие команды, тем временем, изучают эффект Казимира для случаев с другими топологиями, такими, как лист Мебиуса и торообразные объекты.
Но, несмотря на все прилагаемые исследователями усилия, все еще остается много неразрешенных проблем, связанных с эффектом Казимира. В частности, кажущийся простым вопрос о силе Казимира в одиночной полой сфере все еще остается животрепещущим. Даже нет уверенности, будет ли эта сила притягивающей или отталкивающей. Сам Генрих Казимир размышлял над этой проблемой в 1953, когда искал стабильную модель электрона.
Об авторе (оригинальной
статьи)
Астрид Ламбрехт (Astrid Lambrecht) работает в
Лаборатории Кастлер Броссел (Kastler Brossel):
Laboratoire
Kastler Brossel, Université Pierre et Marie Curie, Ecole Normale
Supérieure, Centre National de Recherche Scientifique, Campus
Jussieu, Case 74, F-75252 Paris cedex 05, France, email lambrecht@spectro.jussieu.fr
Для более глубокого
ознакомления:
M Bordag, U Mohideen and V M
Mostepanenko 2001 New developments in the Casimir effect
H B Chan et al. 2001 Nonlinear micromechanical Casimir
oscillator
F Chen and U Mohideen 2002 Demonstration of the lateral Casimir
force
C Genet, A Lambrecht and S Reynaud 2000 Temperature dependence of
the Casimir force between metallic mirrors
S K Lamoreaux 1997 Demonstration of the Casimir force in the 0.6
to 6 micrometer range
K A Milton 2001 The Casimir Effect: Physical Manifestations of Zero-point Energy (World Scientific, Singapore)
Сила из пустого пространства: эффект Казимира
Авторы: Umar Mohideen (U. California at Riverside) Пояснение: Этот маленький шарик дает основания предполагать, что Вселенная будет вечно расширяться. Шарик, имеющий размер немного больше одной десятой миллиметра, движется к гладкой пластинке в результате действия флуктуаций энергии в вакууме. Это притяжение известно как эффект Казимира, названный по имени его первооткрывателя. 50 лет назад он пытался понять, почему жидкости, подобные майонезу, текут так медленно.
Пояснение: Этот маленький шарик дает основания предполагать, что Вселенная будет вечно расширяться. Шарик, имеющий размер немного больше одной десятой миллиметра, движется к гладкой пластинке в результате действия флуктуаций энергии в вакууме. Это притяжение известно как эффект Казимира, названный по имени его первооткрывателя. 50 лет назад он пытался понять, почему жидкости, подобные майонезу, текут так медленно.Сейчас появляется все больше свидетельств того, что большая часть энергии Вселенной находится в неизвестной форме, называемой темной энергией. Форма и происхождение темной энергии практически неизвестны, однако утверждается, что она связана с флуктуациями вакуума, похожими на эффект Казимира, но каким-то образом возникающими в самом пространстве. Эта огромная и загадочная темная энергия должна отталкивать все вещество и поэтому, вероятно, может быть причиной бесконечного расширения Вселенной. Изучение флуктуаций вакуума находится на переднем крае исследований не только потому, что оно служит для лучшего понимания нашей Вселенной, оно важно также для предотвращения слипания деталей миниатюрных механизмов.
Смотрите так же Американские физики получили нечто из ничего
