Броуновское движение
Во второй половине ХХ века в научных кругах разгорелась нешуточная дискуссия о природе атомов. На одной стороне выступали неопровержимые авторитеты, такие как Эрнст Мах (см. Ударные волны), который утверждал, что атомы — суть просто математические функции, удачно описывающие наблюдаемые физические явления и не имеющие под собой реальной физической основы. С другой стороны, ученые новой волны — в частности, Людвиг Больцман (см. Постоянная Больцмана) — настаивали на том, что атомы представляют собой физические реалии. И ни одна из двух сторон не сознавала, что уже за десятки лет до начала их спора получены экспериментальные результаты, раз и навсегда решающие вопрос в пользу существования атомов как физической реальности, — правда, получены они в смежной с физикой дисциплине естествознания ботаником Робертом Броуном.
Еще летом 1827 года Броун, занимаясь изучением поведения цветочной пыльцы под микроскопом (он изучал водную взвесь пыльцы растения Clarkia pulchella), вдруг обнаружил, что отдельные споры совершают абсолютно хаотичные импульсные движения. Он доподлинно определил, что эти движения никак не связаны ни с завихрениями и токами воды, ни с ее испарением, после чего, описав характер движения частиц, честно расписался в собственном бессилии объяснить происхождение этого хаотичного движения. Однако, будучи дотошным экспериментатором, Броун установил, что подобное хаотичное движение свойственно любым микроскопическим частицам, — будь то пыльца растений, взвеси минералов или вообще любая измельченная субстанция.
Лишь в 1905 году не кто иной, как Альберт Эйнштейн, впервые осознал, что это таинственное, на первый взгляд, явление служит наилучшим экспериментальным подтверждением правоты атомной теории строения вещества. Он объяснил его примерно так: взвешенная в воде спора подвергается постоянной «бомбардировке» со стороны хаотично движущихся молекул воды. В среднем, молекулы воздействуют на нее со всех сторон с равной интенсивностью и через равные промежутки времени. Однако, как бы ни мала была спора, в силу чисто случайных отклонений сначала она получает импульс со стороны молекулы, ударившей ее с одной стороны, затем — со стороны молекулы, ударившей ее с другой и т. д. В результате усреднения таких соударений получается, что в какой-то момент частица «дергается» в одну сторону, затем, если с другой стороны ее «толкнуло» больше молекул — в другую и т. д. Использовав законы математической статистики и молекулярно-кинетической теории газов, Эйнштейн вывел уравнение, описывающее зависимость среднеквадратичного смещения броуновской частицы от макроскопических показателей. (Интересный факт: в одном из томов немецкого журнала «Анналы физики» (Annalen der Physik) за 1905 год были опубликованы три статьи Эйнштейна: статья с теоретическим разъяснением броуновского движения, статья об основах специальной теории относительности и, наконец, статья с описанием теории фотоэлектрического эффекта. Именно за последнюю Альберт Эйнштейн был удостоен Нобелевской премии по физике в 1921 году.)
В 1908 году французский физик Жан Батист Перрен (Jean-Baptiste Perrin, 1870–1942) провел блестящую серию опытов, подтвердивших правильность эйнштейновского объяснения феномена броуновского движения. Стало окончательно ясно, что наблюдаемое «хаотичное» движение броуновских частиц — следствие межмолекулярных соударений. Поскольку «полезные математические условности» (по Маху) не могут привести к наблюдаемым и совершенно реальным перемещениям физических частиц, стало окончательно ясно, что спор о реальности атомов окончен: они существуют в природе. В качестве «призовой игры» Перрену досталась выведенная Эйнштейном формула, которая позволила французу проанализировать и оценить среднее число атомов и/или молекул, соударяющихся с взвешенной в жидкости частицей за заданный промежуток времени и, через этот показатель, рассчитать молярные числа различных жидкостей. В основе этой идеи лежал тот факт, что в каждый данный момент времени ускорение взвешенной частицы зависит от числа соударений с молекулами среды (см. Законы механики Ньютона), а значит, и от числа молекул в единице объема жидкости. А это не что иное, как число Авогадро (см. Закон Авогадро) — одна из фундаментальных постоянных, определяющих строение нашего мира.
ИзВ любой среде существуют постоянные микроскопические флуктуации давления. Они, воздействуя на помещенные в среду частицы, приводят к их случайным перемещениям. Это хаотическое движение мельчайших частиц в жидкости или газе называется броуновским движением, а сама частица - броуновской.
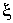 , среднее значение которой равно нулю:
, среднее значение которой равно нулю: 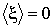 . Тогда можно записать уравнение движения
броуновской частицы в направлении выбранной оси
. Тогда можно записать уравнение движения
броуновской частицы в направлении выбранной оси 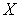 в виде
в виде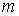 - масса броуновской частицы,
- масса броуновской частицы, 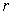 - коэффициент вязкого трения броуновской
частицы в жидкости. Умножим правую и левую часть уравнения
- коэффициент вязкого трения броуновской
частицы в жидкости. Умножим правую и левую часть уравнения 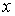 и воспользуемся равенством:
и воспользуемся равенством: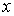 и силы
и силы 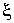 являются взаимно статистически независимыми и
среднее значение их произведения равно нулю:
являются взаимно статистически независимыми и
среднее значение их произведения равно нулю: 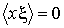 . Кроме того, на основании формулы
. Кроме того, на основании формулы 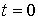 броуновская частица находится в положении с
координатой
броуновская частица находится в положении с
координатой 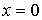 и поэтому
и поэтому 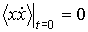 . Для этого случая решение уравнения
. Для этого случая решение уравнения 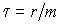 является очень небольшой величиной по
сравнению со временем наблюдения броуновской частицы. При
является очень небольшой величиной по
сравнению со временем наблюдения броуновской частицы. При 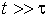 , что соответствует случаю установившегося
броуновского движения, имеем
, что соответствует случаю установившегося
броуновского движения, имеем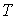 и уменьшается с возрастанием коэффициента
вязкого трения
и уменьшается с возрастанием коэффициента
вязкого трения 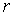 .
.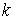 и вычислить значение постоянной Авогадро
и вычислить значение постоянной Авогадро 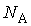 , совпадающие по величине с их значениями,
полученными другими методами.
, совпадающие по величине с их значениями,
полученными другими методами.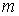 , закрепленной на пружине жесткостью
, закрепленной на пружине жесткостью 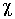 . Коэффициент вязкого трения частицы в
жидкости считать равным величине
. Коэффициент вязкого трения частицы в
жидкости считать равным величине 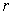 . В начальный момент времени частица находится
в положении с координатой
. В начальный момент времени частица находится
в положении с координатой 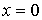 .
.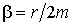 - коэффициент затухания,
- коэффициент затухания, 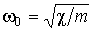 - собственная частота колебаний частицы,
- собственная частота колебаний частицы, 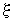 - случайная сила, среднее значение которой
равно нулю:
- случайная сила, среднее значение которой
равно нулю: 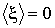 .
.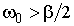 . Тогда с учетом начального условия
. Тогда с учетом начального условия 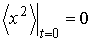 решение этого уравнения можно записать в
форме:
решение этого уравнения можно записать в
форме: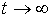 величина квадрата средних флуктуаций
координаты частицы
величина квадрата средних флуктуаций
координаты частицы 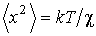 , что соответствует выражению, полученному в
задаче 5.4.
, что соответствует выражению, полученному в
задаче 5.4.
Из
А.Д. Суханов. Обобщенное соотношение неопределенностей "координата-импульс" в квантовой механике и теории броуновского движения. //Теор. и матем. физика. 2004. V.139. No.1.,C.129.
Показано, что обобщенные соотношения неопределенностей Шредингера имеют смысл фундаментальных ограничений на характеристики пространства состояний в любой теории вероятностного типа. К таким теориям относятся как квантовая механика, так и теория броуновского движения при произвольных промежутках времени. Проведено сравнение соотношения неопределенностей "координата-импульс" в этой теории с аналогичным соотношением неопределенностей для микрочастицы в состоянии гауссова волнового пакета. Установлено, что при серьезном различии в математических аппаратах двух теорий между ними наблюдается концептуальное сходство. Оно проявляется в альтернативных режимах - малые времена в одной теории соответствуют большим временам в другой теории, и наоборот, причем в каждой из этих теорий существенную роль играет неконтролируемое воздействие либо квантового, либо теплового типа.
Броуновское движение и диффузия - как принципиально недетерминированные процессы
Представляя броуновское движение и диффузию - как результат соударений атомов, молекул или тел, соизмеримых в первыми по массе, можно было бы предположить теоретическую вычисляемость траекторий, исходя из некоторых начальных условий. Нужно заметить, что все зависимости, описывающие эти процессы, конечно же, не дают решение для траекторий :) а лишь - зависимость среднеквадратичного смещения. Но, учитывая, что атомы, на самом деле - не идеальные упругие шарики, а вектор взаимодействия с другим атомом будет неопределенным в силу соотношения неопределенностей "координата-импульс" в квантовой механике (в зависимости от распределения плотности электронов в момент взаимодействия), то и результат взаимодействия не возможно рассчитать не статистически.
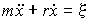 ,
,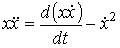 .
.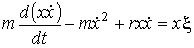 .
.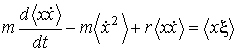 .
.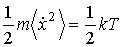 .
.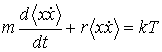 .
.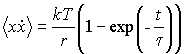 ,
,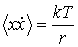 .
.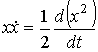 ,
,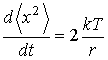 .
.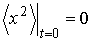 , дает
, дает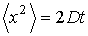 ,
,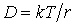 .
.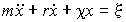
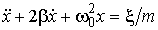 ,
,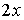 и, воспользовавшись равенствами
и, воспользовавшись равенствами 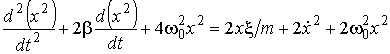 .
.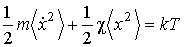
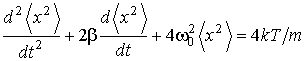 .
.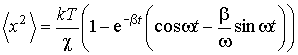 ,
,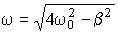 .
.