Макро-интерференция - удивительный эксперимент Дёмина

Макро-интерференция - удивительный эксперимент Дёмина

Путенихин П.В.
m55@mail.ru

Эксперимент Дёмина

Эксперимент с двумя щелями и возникающая в нём интерференция, как отметил Фейнман, "заключает в себе сердце квантовой механики" [1] и является квинтэссенцией принципа квантовой суперпозиции. Действительно, попытки просто описать это явление, приводят к довольно противоречивым и даже фантастическим выводам. Изначально явление интерференции считалось присущим лишь свету, фотонам. Но в дальнейшем обнаружилось, что интерференционную картину создают и электроны, и нейтроны, атомы и даже их довольно крупные соединения. В одной из своих работ Пенроуз в шутливой форме вывел довольно невероятное следствие формализма квантовой механики о наличии состояния суперпозиции у макрообъектов:

"Правила квантовой механики, насколько можно судить, утверждают, что и крикетные шары, и слоны должны вести себя описанным выше странным образом, где различные альтернативные возможности могут каким-то образом образовывать "суммы" состояний с комплексными весами! [2].

К появлению интерференционной картины, как следует из квантовых уравнений, приводит именно суперпозиционное состояние частицы. То есть, формально нет никаких запретов на интерференцию суперпозиционных состояний не только фотонов, но и макрообъектов, в том числе, крикетных шаров, слонов, людей и шредингеровского кота.

Тема, несомненно, трудная, но и весьма интересная. В этой связи обратимся к одному реально проведённому эксперименту, результаты которого уже сложно оценить традиционным «неоднозначные». Это эксперимент, проведённый С.В.Дёминым и описанный в статье «Волны вероятности в стохастических процессах» [3]. В двух словах можно сказать, что эксперимент показал весьма заметную интерференцию металлических шариков, хотя сам автор такие выводы делает как предположительные.

Рассмотрим суть эксперимента вкратце, при необходимости несущественно изменяя расположение цитируемых фрагментов: некоторые рисунки перемещены туда, где даётся ссылка на них.

Во вводной части автор отметил со ссылкой на публикации, что

«Зарегистрированные в недавних экспериментах эффекты противоречат и постулатам теории относительности, и обыденному здравому смыслу, что проявляется, в частности, в нарушении принципа причинности. Однако считается, что это противоречие, по крайней мере, не выходит за рамки законов микромира, несмотря на макроскопический характер наблюдаемых эффектов…»

Затронув вопросы нелокальности, он отмечает, что:

«По мнению большинства физиков, способностями к такому «сверхъестественному» общению наделены только микрочастицы, и эти их способности не могут быть использованы в создаваемых нами технических устройствах».

И делает предположение о том, что:

«Парадоксы, иллюстрирующие проявления нелокальности через регистрацию неклассических (квантовых) корреляций пространственно-временных переменных …, вытекают из ортодоксальной интерпретации квантовой механики».

Далее он справедливо указывает:

«Пожалуй, к каким-либо кардинальным изменениям в этой науке могло бы привести появление новых опытных данных, не вписывающихся в устоявшиеся физические концепции».

Из чего становится очевидным направленность проведённого им эксперимента:

«Возможно, описанные в статье эксперименты указывают на ту область, в которой следует искать такие данные».

Не приводя ссылок и описаний, он лишь указывает на ранее проведённые в этом направлении опыты, и задаётся, несомненно, фундаментальными вопросами о причинности:

«Толчком к опытам, которые были начаты автором статьи много лет назад, послужил крамольный, с точки зрения ортодоксальной физики, вопрос: нарушается ли принцип макроскопической причинности? Влияет ли будущее состояние макрообъекта при каких-то условиях на его состояние в прошлом?»

Судя по следующему заключению, эти опыты дали довольно спорный ответ, правда, в предположительном тоне о влиянии будущего на прошлое:

«Именно результаты опытов, которые можно было рассматривать в качестве утвердительного ответа на этот вопрос, заставили автора статьи искать у макрообъектов свойства, напоминающие квантово-волновые свойства микрочастиц, что привело к наблюдению явлений, подобных интерференции в двухщелевом эксперименте, а также к регистрации «дискретных»… энергетических состояний макросистемы, соответствующих наблюдаемым «интерференционным» явлениям».

Как видим, цели в высшей степени интересные. В разделе о постановке задачи автор их конкретизирует:

«Обнаружить закономерности, подобные квантово-механическим, в движении макрообъектов проще всего, изучая случайные процессы».

Основу такого подобия автор, вполне логично, видит в том, что макрообъекты должны обладать в некоторой степени такими же свойствами, какими обладают и квантовые частицы:

«Во-первых, волновые свойства частиц предполагают «либо принципиальное отсутствие траектории их движения (что трудно себе наглядно представить, но на чем настаивает большинство физиков), либо хоть какую-то ее неопределенность, имеющую место, например, при случайном движении.

Во-вторых, чтобы нарушения принципа причинности, которые могут возникать в силу временной нелокальности протекающих процессов, не приводили к неразрешимым логическим парадоксам, всякое такое нарушение должно находить разумное объяснение».

Здесь, правда, следует отметить ошибочные взгляды автора на причинность, хотя и со ссылкой на классические понимания:

«Допустим, причина некоего явления находится в будущем. Если это явление можно рассматривать как флуктуацию в каком-либо стохастическом процессе, то подобное объяснение вполне удовлетворяет и требованию разумности, и классическому пониманию реальности».

Ни в каком процессе нет и быть не может причинного влияния будущего на прошлое. Стохастические, в смысле случайных совпадений, влияниями как таковыми не являются. Это, пожалуй, единственное серьёзное замечание по проведённому автором эксперименту, если не считать приведённые ниже замечания по глубине эксперимента.

Технически содержание эксперимента представляет собой регистрацию движения шариков по наклонной плоскости:

«Для эксперимента по поиску подобия квантовых закономерностей в стохастических процессах было выбрано блуждающее движение шариков по наклонной плоскости – некий аналог известной доски Гальтона (см. рис.1).

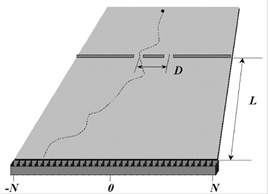
Рис. 1. Наклонная доска для исследования волновых явлений в стохастических процессах

Шарики, поверхность которых не является идеально сферической, скатывались по плоскости, наклоненной под определенным углом, по случайной траектории, расположенной внутри некоторого конуса, после чего попадали в расположенные в нижней части плоскости ячейки. При этом распределение шариков по ячейкам, как известно, должно подчиняться закону Гаусса (см. рис.2).

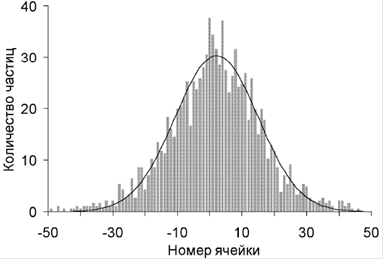
Рис. 2. Пример распределения частиц, скатившихся по наклонной доске. Сплошной линией показана аппроксимация распределением Гаусса.

Характер случайных отклонений от теоретически рассчитанной кривой нормального распределения составил основной предмет изучения в данной работе».

Экспериментальные данные получены следующим путём:

«Для моделирования явлений, подобных интерференционным, в средней части наклонной плоскости устанавливалось препятствие с двумя узкими отверстиями, через которые скатывающиеся шарики могли попадать на нижнюю половину плоскости (см. рис.1)».

Эксперимент проводился в различных режимах: изменялись расстояние между щелями, число скатываемых шариков, угол наклона доски, при которых подсчитывалось число шариков, упавших в ячейки. Полученные при этом результаты обрабатывались аналитически. Наибольший интерес представляют значения функции F(n), в которой f_e(n) иf_a(n) – распределение этих шариков по ячейкам, измеренное в эксперименте и аппроксимированное нормальным распределением:

«После этого были найдены разности между экспериментальными значениями и значениями, рассчитанными в результате аппроксимации (см. гист.F на рис.3 и 4):

F(n) = f_e(n) - f_a(n).

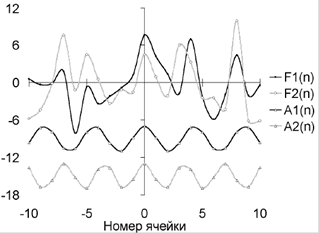
Рис. 3. Отклонение реального распределения от распределения Гаусса при расстоянии между отверстиями 32мм - F1(n) и 40мм - F2(n). Кривые A1(n) и A2(n) показывают теоретически рассчитанное положение максимумов для интерференции волн длиной 2мм.

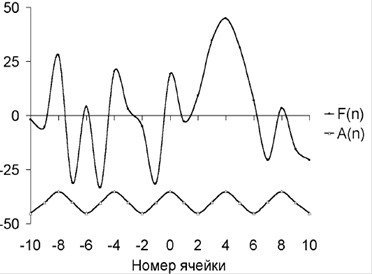
Рис. 4. Отклонение реального распределения от распределения Гаусса при расстоянии между отверстиями 22 мм во втором эксперименте - F(n). Кривая A(n) - теоретически рассчитанное положение максимумов для интерференции волн длинной 1,04 мм».

На этом этапе уже получен визуальный результат, который вне всяких сомнений можно называть, как минимум, удивительным. Даже с учетом довольно-таки не ровного графика интерференции, сам факт неравномерного и при этом определённо периодического распределения шариков по ячейкам заслуживает самого пристального внимания и анализа.

В продолжение эксперимента автор вполне закономерно проводит дополнительный анализ результатов:

«Поскольку полученные отклонения от нормального распределения выглядели более или менее периодическими, была сделана попытка оценить длину волны, которая при прохождении через соответствующие отверстия давала бы интерференционную картину с аналогичным положением максимумов и минимумов. Для этого к полученным рисункам были добавлены графики функций, положение экстремумов которых точно соответствует расчетному при интерференции волн той или иной длины».

Приведены соответствующие аналитические выражения для вычисления искомой длины волны и гистограммы распределения количества шариков по их скорости при различной величине наклона плоскости.

Результаты, прямо скажем, выглядят просто как невероятные. Это осознаёт и автор, поэтому раздел «Обсуждение» начинает с осторожного предположения о достоверности полученных результатов:

«Даже беглый взгляд на представленные диаграммы вызывает желание спросить: а какова достоверность полученных результатов? И, соответственно: а имеют ли место вообще эти результаты и есть ли предмет для разговора? Не стоило ли проявить большую аккуратность при постановке опытов или хотя бы просто увеличить количество измерений? Корректно ли вообще делать какие-либо выводы на такого рода материале, тем более выводы, претендующие на фундаментальность?»

Несомненно, что в таких серьёзных вопросах осторожность никогда не помешает. На основе только одного эксперимента легко сделать ошибочные выводы. Поэтому отвечает на этот вопрос он также в предположительно-утвердительном тоне:

«Возможно, в основе всей данной работы лежит ответ именно на этот вопрос».

Он указывает на возможную достоверность результатов, поскольку с одной стороны:

«Механика Ньютона прекрасно описывает движение макроскопических тел. Наивно ожидать, что результаты простейших экспериментов, подобных описанным выше, придут с ней в открытое противоречие. Такого рода противоречия наверняка были бы замечены много ранее».

Но тут же справедливо допускает и недостаточность этого:

«Следует, однако, заметить, что эта механика имеет дело исключительно с детерминистским аспектом движения. Даже описание случайных процессов в классической физике в конечном итоге сводится к строгому определению границ, в которые должна попасть та или иная физическая величина».

Известно, что едва ли не главной проблемой любого эксперимента является его погрешность (шум), снижающая его достоверность:

«Считается аксиомой то, что шум, сопровождающий любой эксперимент, не может нести в себе никакой полезной информации, и главная задача экспериментатора в том, чтобы избавиться от этого шума, произведя, например, достаточное количество измерений».

Всё верно, множество экспериментов в наши дни отсеиваются именно по этому показателю. Хотя, возможно, иной раз чрезмерно ретиво. В данном же случае автор словно предлагает читателю самому сделать оценку достоверности:

«Эта работа написана для тех, кто готов заглянуть за кулисы законов Ньютона, зайти на территорию, которая всегда в науке считалась запретной».

Анализируя полученные результаты, очевидно, свидетельствующие в пользу их достоверности, автор отмечает, что

«…как и ожидалось, никакой принципиальной разницы в результатах опытов со ста, тысячью или десятью тысячами измерений замечено не было. В двухщелевом эксперименте, с одной стороны, с первых же измерений наблюдались отклонения от нормального распределения, которые выглядели более или менее периодическими, напоминая картину интерференционных максимумов и минимумов, а с другой стороны, по мере накопления данных эти отклонения постепенно уменьшались, впрочем, так окончательно и не исчезая».

Здесь следует заметить, что «окончательно не исчезая» может оказаться главной проблемой эксперимента. Вполне можно допустить, что при достаточно большом числе измерений отклонения могли исчезнуть.

«Некоторые из симметричных локальных экстремумов на гистограммах были очень устойчивы и соответствовали довольно значительным по величине отклонениям от значений, полученных в результате аппроксимации экспериментальной гистограммы колоколообразной кривой нормального распределения».

Тем не менее, для большей достоверности этих наблюдений необходимы дополнительные измерения в различных режимах, с ещё большим количеством шариков и с их отсеиванием на входе в щели, о чём будет сказано ниже. В оправдание, автор отмечает, хотя, на мой взгляд, чрезмерно принижая достоверность эксперимента, что:

«В этой статье приводятся не самые убедительные в этом отношении данные, потому что ее объем не позволяет привести все полученные результаты».

С чем трудно согласиться (в пользу эксперимента!), так это с ответом на вопрос:

«Можно ли считать относительную периодичность следования пиков на гистограммах достаточно убедительным свидетельством того, что мы имеем дело с неким подобием интерференционных явлений? Скорее всего нет».

Ответ, по всей видимости, является попыткой уйти от чрезмерной и огульной критики, которая здесь весьма вероятна. На мой взгляд, ответом должно быть всё-таки «скорее всего, да». Именно по причине такой же «неуверенной» интерпретации полученных результатов отметаются результаты экспериментов Маринова по проверке специальной теории относительности. Хотя факт «угадывания» в этих экспериментах направления движения ИСО плохо объясняется простым совпадением. В случае эксперимента по интерференции шариков точно так же нужно сильно постараться, чтобы объяснить периодическую неравномерность попадания шариков в ячейки. Простым случайным совпадением здесь вряд ли обойтись.

Вместе с тем, автор указывает на другую особенность эксперимента:

«Пожалуй, именно построение распределения скатывающихся частиц по их средней скорости дало наиболее неожиданные результаты. Внешне движение шариков выглядело совершенно хаотичным, и трудно было себе представить, по какой причине их средняя скорость могла бы иметь два ярко выраженных предпочтительных значения (см. рис.6).

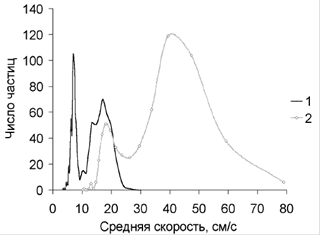
Рис. 6. Распределение частиц диаметром 2мм по скоростям в двух экспериментах с различной величиной наклона плоскости».

…на кривой распределения появились дополнительные пики, которые при достаточно большом числе измерений (1500 частиц) стали совершенно отчетливыми и, вне всякого сомнения, достоверными, далеко выходящими за пределы случайных отклонений…»

Конечно, удивление автора, на первый взгляд, понятно. По какой причине скорости шариков имеют некоторые предпочтительные значения? Но здесь можно сделать, например, такое простое умозрительное предположение. А не связано ли это с количеством щелей, ведь их тоже две, как и пиков на графике распределения? Что это за связь, предположить сложно, тем более что на диаграмме 7 таких пиков заметно больше.

«С другой стороны, такое поведение физической системы хорошо укладывается в первоначально высказанное предположение о том, что квантовые закономерности проявляются в макромире исключительно в стохастических процессах. Чем больше элемент случайности, тем ближе поведение системы к тому, что мы привыкли наблюдать в микромире».

Такое замечание является крайне важным. Действительно, проводится параллель, тождество в поведении квантовых частиц и макрообъектов. И эта параллель может иметь серьёзные последствия. Такое подобие даёт основание предположить, что квантовая интерференция не является следствием суперпозиции, то есть прохождения частицы одновременно через две щели. Это очень серьёзное предположение, приводящее к далеко идущим выводам, можно сказать, фундаментальным. Невозможно вообразить, чтобы шарик, имеющий достаточно большие размеры, прошёл одновременно через две щели.

Далее в случае с шариками можно проверить справедливость известного правила квантовой механики -  «знание о пути фотона разрушает интерференционную картину». Для этого нужно вести явное наблюдение за шариками. Факт наблюдения, очевидно, будет оказывать крайне незначительное влияние на траекторию. Но, согласно правилу, интерференция должна быть разрушена. Причём эти две ситуации можно повторять сколько угодно. Но даже в случае выполнения этого правила в отношении шариков, остаётся очевидным ответ: шарик не может одновременно пройти через две щели, это из разряда мистики. Но тогда неизбежен вывод: возникновение интерференции не связано с суперпозиционным состоянием шарика и, следовательно, оно также может быть не связано и с суперпозицией квантовых частиц.

В разделе «Заключение» автор работы выражает надежду в отношении полученных результатов, что:

«…выводы, которые из них следуют, сделаны не на пустом месте и не являются следствием тех или иных недостатков, которые, конечно же, имели место в силу слабого материального обеспечения экспериментов. После просмотра всего представленного материала остается впечатление, что, несмотря на малоправдоподобность следующих из него выводов, вероятность того, что он отражает реально существующие закономерности, все же больше вероятности того, что в его основе лежат многократно повторенные совпадения и незамеченные ошибки».

Мы не будем анализировать приведённую далее, как он её сам назвал, фантастическую гипотезу автора, объясняющую наличие волновых функций у макротел, поскольку нас намного больше и главным образом интересует фактическая сторона. Наличие интерференционных флуктуаций у падающих шариков во вполне корректно проведённых экспериментах вряд ли можно просто так оставить без внимания.

Всё верно, однако…

Следует ещё раз отметить, что все выкладки, аргументация и полученные данные корректны, логичны и не вызывают нареканий. Но так уж устроен этот странный мир – у каждой, даже самой хорошей идеи обязательно найдётся «но». Здесь это «но» относится не к собственно проведённому эксперименту и его анализу, а к его объёму. Этот эксперимент следует считать первым и верным шагом в выбранном направлении. Однако, правильнее всё-таки оценить это направление в целом, а не вырезать из него фрагменты. В общем виде задачу экспериментов этого типа следует сформулировать, как стремление провести наиболее полную параллель между рассмотренным явлением в макромире и в мире квантовых частиц. Весьма ярко и наглядно имитация поведения квантовых частиц в макромире  показана, например, в статье Заречного в примере с пулеметом:

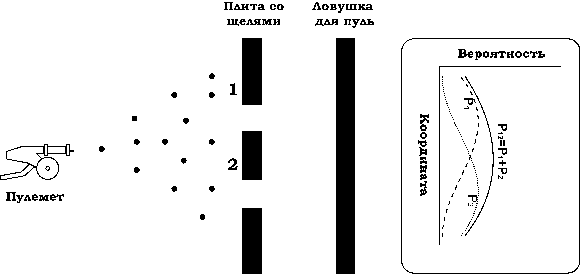
Рис.7. При наличии двух щелей поток пуль из пулемёта не образует интерференционную картину [4].

Легко заметить принципиальное сходство этого мысленного эксперимента с реальным физическим экспериментом Дёмина (с точностью до флуктуаций нормального распределения). Так на что здесь следует особо обратить внимание?

В научной и учебной литературе описание эксперимента с двумя щелями практически всегда сопровождается демонстрацией прохождения частиц, когда одна из щелей закрыта. При этом интерференция сразу же нарушается, независимо от того, какая из щелей закрыта. Следовательно, для полноты и максимального соответствие обычному двухщелевому эксперименту следует дополнить рассмотренный эксперимент Дёмина двумя дополнительными измерениями – с каждой из щелей в отдельности. Вот в этом случае и может возникнуть то самое «но». Важно, что в том случае, если флуктуации останутся, то ни о какой интерференции уже говорить не придётся! Это будет полным и безоговорочным провалом эксперимента и всех следовавших из него выводов. Напротив, в случае, если нормальные распределения будут центрироваться напротив каждой из одиночных щелей без каких-либо флуктуаций, то значимость эксперимента повысится до предела, до максимальной достоверности. Это будет ещё одним, дополнительным и весьма сильным доводом в пользу реальности интерференционных флуктуаций. Это будет настолько убедительный довод, что уже никакие погрешности эксперимента не смогут принизить его значимость. Действительно, наличие и отсутствие флуктуаций в разных сериях эксперимента снимает всякие сомнения в том, что они – реальность, а не шумы, погрешности измерений. Во всех сериях условия эксперимента одинаковы, поэтому шумы и погрешности – тоже одинаковы.

Кроме этого, из описания эксперимента неясно, как ведут себя шарики, не попавшие «прямиком» в щель. Скорость их при столкновении с перегородками падает до нуля, после чего, возможно, они просто скатываются в щели? В этом случае также просматривается отклонение от стандартного эксперимента с фотонами или другими квантовыми частицами. Фотоны, например, на перегородке просто поглощаются и не участвуют в создании интерференционной картины. Для более реалистичных измерений и большего сходства со стандартной интерференцией следует, видимо, эти прямиком не попавшие в щели шарики удалять с доски, не давая им упасть через щели.

Автоматизация измерений

Очевидно, что трудоёмкость проведения эксперимента возрастёт с увеличением числа измерений, и вследствие добавления, по меньшей мере, двух дополнительных серий с закрытыми поочередно щелями. Однако, можно указать на технологические возможности для автоматизации измерений и увеличения их числа до любой мыслимой величины. Во-первых, шарики можно сбрасывать на щели поочередно, с интервалом не более чем время их движения до края доски. В этом случае упавшие шарики можно сразу же вернуть для повторного броска, что позволит уменьшить их число до нескольких десятков или сотен. Такой «перенос» шариков снизу вверх может быть легко автоматизирован.

Подсчёт шариков и координаты их «приземления» легко вести с помощью веб-камеры и соответствующего программного обеспечения. В реальном режиме времени камера делает снимки, из которых программно извлекается информация о точке приземления шариков и даже их траектории. В этом случае координата будет практически непрерывной, а не определяться числом ячеек в конце доски.

Как вариант, регистраторами могут быть фотодетекторы, используемые в сканерах, поскольку разрешение у них достаточно высокое – многие сотни и тысячи пикселей на дюйм. В этом случае усложняется аппаратная часть, с помощью которой сигналы от детекторов преобразуются в цифровой вид.

Шарики, не попавшие «прямиком» в щель, удаляются с доски через соответствующие отверстия и не принимают участия в формировании интерференционной картины.

Таким образом, экспериментальная доска может иметь примерно такой вид:

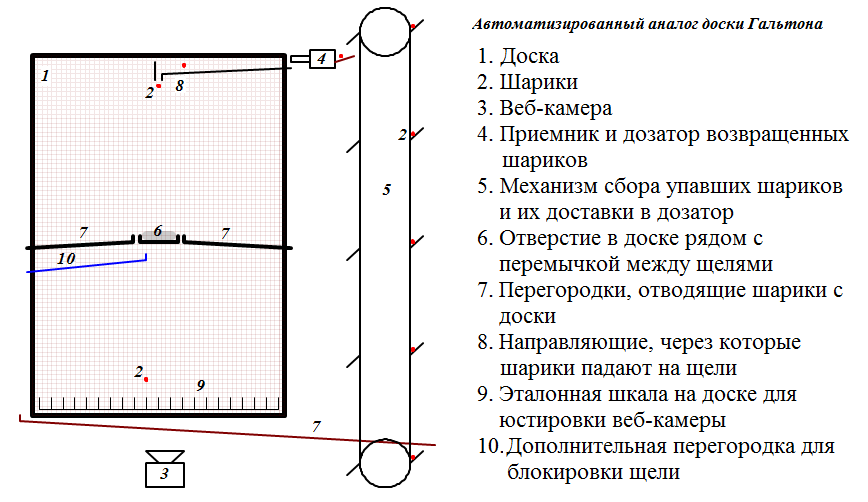
Рис.8. Интерференционная доска с автоматическим сбором информации

Такая конструкция доски позволяет до предела уменьшить роль экспериментатора в сборе данных, всё производится автоматически. Шарики 2 подаются с заданным интервалом дозатором-приемником 4 в направляющие 8, через щель которого они затем попадают на доску 1 и скатываются к двум щелям 7-7. Пройдя через щель, шарик падает на нижнюю перегородку 7, по которой скатывается к механизму сбора 5 и доставки шариков к дозатору-приемнику 4, после чего шарик вновь может быть направлен на доску. При падении на нижнюю перегородку шарик проходит мимо эталонной шкалы 9, где попадает в объектив веб-камеры 3. На снимке можно будет точно вычислить координату упавшего шарика.

Шарики, которые прямиком не попали в одну из щелей, скатываются по отводящим перегородкам 7 и вновь направляются в дозатор 4. Шарики, попавшие между щелями на среднюю перегородку, удаляются с доски через отверстие 6, после чего также направляются в дозатор 4.

Для проведения дополнительного эксперимента одна из щелей может быть заблокирована дополнительной перегородкой 10, которая удаляет шарики до того, как они достигнут нижней перегородки 7 и шкалы 9.

При темпе падения шариков один в секунду, что можно считать достаточно медленным, 10 тысяч шариков пройдут через направляющие всего за три часа. Понятно, что до нижнего края дойдут не все, но это можно компенсировать увеличением времени измерений. Необходимое число шариков, видимо, крайне мало, поскольку «в работе» будут находиться одновременно менее чем десяток-другой шариков.

Веб-камера будет «видеть» шарики под некоторым углом в зависимости от их удаления от центра доски. Однако, для программного модуля это незначительная техническая сложность. Зато координаты упавших шариков будут иметь точные значения и графики интерференционных флуктуаций будут практически непрерывными. Для простоты можно напротив щелей установить вторую веб-камеру, которая будет фиксировать момент прохождения шарика через щель. Это позволит вычислить и его скорость и даже траекторию, которую можно аппроксимировать, например, дугой окружности.

Режимы эксперимента могут быть как с традиционным уклоном доски, так и с её строго вертикальным положением. В этом случае шарики будут падать строго отвесно в поле тяготения. Такой эксперимент сам по себе представляет особый интерес и будет довольно сильно напоминать эксперимент с интерференцией атомов рубидия, которые по сравнению с фотонами тоже являются довольно крупными объектами:

«Пучок атомов рубидия … падает под действием гравитационного поля. … две пары перекрывающихся пучков в дальней зоне образуют стандартную интерференционную картину» [5].  

На движение шариков в этом случае уже не будут влиять силы трения и даже точность их формы и качество поверхности.

Сбор данных в реальном режиме времени должен в обязательном порядке производиться в электронную (компьютерную) базу данных. Произведём простую оценку объёма данных этой базы. Каждое измерение целесообразно описывать некоторым набором параметров: номер шарика (замера), координата «приземления» - это основные данные. Вспомогательными данными могут быть: номер щели; момент выхода из щели; момент прохождения нулевой отметки внизу доски; от одной до пяти точек на интервале от щели до нулевой отметки. Другие данные вряд ли нужны. Таким образом, объём базы на один эксперимент составит: 10 000*(2+8)=100 000 записей для шариков, реально достигших нижней веб-камеры. Очевидно, что каждый элемент таблицы (базы) вполне уместится в 2-3 байта машинной памяти. Следовательно, объём бинарной базы не превысит 300 кБ. По современным характеристикам компьютерного оборудования – это крошечный файл. При использовании стандартных баз данных этот объём, конечно, увеличится в десятки раз, но и в этом случае будет достаточно небольшим.

Создание баз данных позволит всем заинтересованным исследователям самостоятельно произвести обработку информации с построением различных гистограмм по собственным соображениям.

Одновременно с заполнением информационной базы можно выводить информацию на экран как в виде интерференционных полос, так и в анимационном виде. Например, полученные в рассматриваемой статье данные можно изобразить в традиционном виде черно-белой интерференционной шкалы:

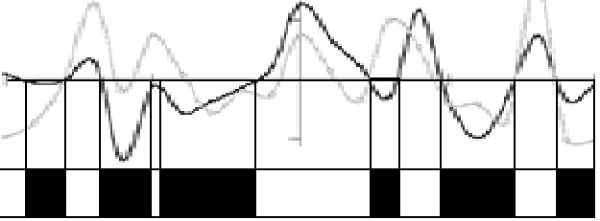
Рис.9. Традиционное изображение интерференционной шкалы, построенное на основе данных рис.3.

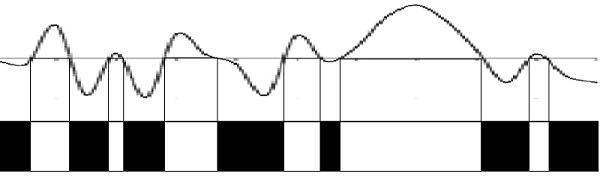
Рис.10. Традиционное изображение интерференционной шкалы, построенное на основе данных рис.4

Такая интерференционная шкала может строиться динамически на экране монитора в процессе сбора данных. Изначально она будет вся черная, затем на ней начнут появляться отдельные узкие светлые полоски, соответствующие каждому упавшему шарику, и, наконец, она примет примерно такой вид, как показано на рисунках.

При необходимости анимированное изображение как телевизионная трансляция может быть изображением доски с веб-камеры, дополненное указанной интерференционной полосой и графиком распределения.

В случае получения положительного экспериментального результата – четко выраженной интерференционной картины при двух открытых щелях и её полного отсутствия при одной открытой щели, возникает интересный вариант продолжения эксперимента в варианте пулемета Заречного рис.7. Если интерференционную картину показали шарики, то было бы упущением не проверить поведение ещё более крупных объектов – пуль. Возможно, что предположение Пенроуза о крикетных шарах не такая уж и шутка? Очевидно, щели должны быть достаточно прочными, из бронированной стали, чтобы пули не разрушали их края, а оружие должно быть не нарезным, чтобы траектории пуль были более случайными.

Литература

1.Боумейстер Д., Экерт А., Цайлингер А., Физика квантовой информации. -
http://quantmagic.narod.ru/Books/Zeilinger/g1.djvu

2.Пенроуз Роджер, Новый ум короля: О компьютерах, мышлении и законах физики: Пер. с англ. / Общ. ред. В.О.Малышенко. - М.: Едиториал УРСС, 2003. - 384 с. Оригинал статьи:     
Roger Penrose, The Emperor"s New Mind. Concerning Computers, Minds and The Laws of Physics. Oxford University Press, 1989.

3.Демин С.В. Волны вероятности в стохастических процессах. Математические структуры и моделирование. 2001. Вып. 8. С. 91-101, URL:          
http://chronos.msu.ru/old/RREPORTS/demin.pdf           
http://www.everettica.org/art/1n.pdf 
http://msm.univer.omsk.su/sbornik/sbornik8/demin.zip

4.Заречный М.И., Квантовая и мистическая картины мира, 2004, URL:           
http://www.sciteclibrary.ru/rus/catalog/pages/8602.html 
http://www.simoron.dax.ru/ 

5.Цыпенюк Ю.М., Соотношение неопределенностей или принцип дополнительности? - М.: Природа, N5, 1999, с.90

6.Путенихин П.В. Макро-интерференция - удивительный эксперимент Дёмина, [рассмотрен эксперимент с небольшими шариками, создающими интерференционную картину], 2015, URL:        
http://samlib.ru/p/putenihin_p_w/demin.shtml