Ячеистая структура нейросети

В природной нейросети нейроны образуют сложные, запутанные связи, протягивая их между активным рецептором и созревающим нейроном в стадии пейсмекерной активности. Реализовать такой сумбур в симуляторе выглядело довольно сложным, поэтому в качестве решения проблемы возникла идея расположить элементы нейросети в виде равномерной решетки. Предполагалось, что это будет способствовать более прогнозируемому ее поведению, особенно если веса связей так же установить равномерными. Но оказалось, что это привело к неожиданным специфическим эффектам, так как взаимное торможение элементов при изменении параметров нейросети привело к генерации серии эффекторных рисунков, тем большим, чем больше взаимный охват связями, а равномерно распределенные веса к неоднозначным состояниям. Разные типы решеток по-разному детектировали примитивы. Гексагональные с более равномерным круговым охватом так же равноценно определяли прямые и наклонные линии. Ортогональные решетки более чувствительны к детектированию прямых вертикальных и горизонтальных линий. Так же выяснилось, что при активации эффектора происходят колебания его уровня возбуждения, которые тем больше, чем более неравномерно он нагружен. При близких значениях порога и уровня торможения возникают пульсации – периодические включения/выключения эффектора.

В результате экспериментов возникло предположение, что генерация эффекторных рисунков при изменении параметров нейросети могла использоваться у древних организмов как примитивный способ контекстного реагирования, если представить, что параметры нейросети у них были не стабилизированы и зависели от общего состояния гомеостаза. Кроме того, изначально нервная система представляла собой просто соединения рецепторных клеток с эффекторными без централизованного управления, потому, что соответствующих отделов просто не было. Можно предположить, что такие сообщества специализированных клеток постепенно объединялись в какие-то структурированные схемы, подобно тому, как выстраивается решетка связей у кристаллов. На базе такой децентрализованной нервной системы формировались затем специализированные отделы. Стало быть, имеет смысл изучить такие схемы, чтобы хотя бы умозрительно представить, как и что из них могло впоследствии появиться.

В качестве конкретного технического решения родилась идея дуплексной компоновки решетки, при которой рецепторы и эффекторы расположены в одном слое, что упрощает и удешевляет реализацию прототипа.

Для демонстрационных моделей статьи использовались конструктор простейших нейросетей и нейросимуляторы, собранные по нескольким типам ячеистых схем соединений.

Обоснование выбора схемы построения нейросимулятора в виде структурированных решеток.

Основная причина, почему была выбрана ячеистая схема соединений элементов в нейросимуляторе – наличие перекрестных активирующих и тормозных связей между элементами и как результат, их взаимовлияние друг на друга, распределяющее получаемые внешние импульсы. Здесь как бы сразу напрашивается прямая аналогия с кристаллической решеткой. Ведь всякая замкнутая система взаимосвязанных элементов приходит к равновесию, и нейроны-эффекторы, связанные взаимным торможением, так же в конечном итоге будут распределять между собой полученные от рецепторов импульсы. Если расположить элементы в виде решетки, то тем самым задаются пути возможного распространения импульса. Это может существенно упростить  реализацию прототипа в виде физической «нейроплаты», где все дорожки связей изначально проведены с разрывами, заполненными например специальным материалом. Если придумать технологию его модификации, чтобы при «обучении» в одном случае он становился проводником, а в другом диэлектриком, тем самым закрепляя связь с заданным весом или окончательно ее разрывая, то предположительно это будет проще, чем разработка технологии «проращивания» связей. В программной реализации аналогичный подход означает поставить вес установленной по умолчанию виртуальной связи больше нуля. Здесь так же упрощение будет в отсутствии необходимости разработки «модуля ветвления». Еще один важный довод состоит в том, что при структуризации связей появляется возможность построения вложенных одна в другую пары решеток – дуплексный тип, о котором будет рассказано ниже более подробно. Его особенность в том, что в одних узлах решетки располагаются рецепторы, а в других – эффекторы. Такая компоновка при реализации в виде интегральной микросхемы позволяет сократить в 2 раза число элементов, и кроме того, начать обрабатыватьг сигнал сразу в первом же слое.

Вариантов решеток может быть много, но у всех есть общий принцип построения: копирование базового элемента с заданным шагом. При этом возможны 2 типа построения: двойная решетка из пары расположенных друг против другая рецепторной и эффекторной, а также дуплексный тип, где рецепторы и эффекторы расположены в одном слое. Ниже рассмотрим несколько вариантов таких компоновок.

Варианты схем соединения рецептор-эффектор

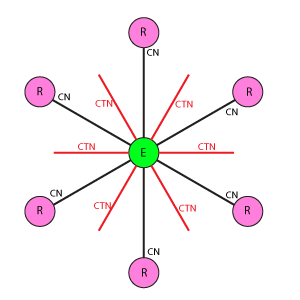
Во всех схемах приняты следующие условные обозначения:

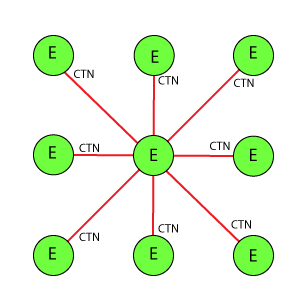
Е: Кружок в центре базового блока, обозначающий эффектор.

R: Кружки, расположенные по вершинам фигуры базового блока вокруг эффектора, обозначающие рецепторы.

Линия между Е(эффектор) и R(рецептор): Основная связь между рецепторами и эффекторами. CN показывает значение веса связи.

Линия между Е(эффекторами): Тормозная связь между эффекторами, имитирует взаимное (латеральное) торможение между нейронами, связанными с рецепторами. CTN показывает значение веса связи.

Дуплексная схема DK6-3

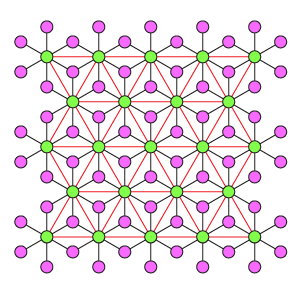
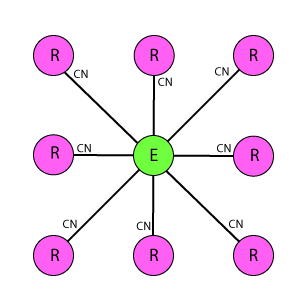
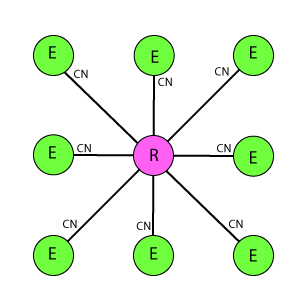
Гексагональная дуплексная решетка, где один эффектор связан с 6 рецепторами, и один рецептор связан с 3 эффекторами. Эффекторы имеют взаимное торможение, где каждый тормозит 6 ближайших соседних.

Дуплексная схема DK3-6

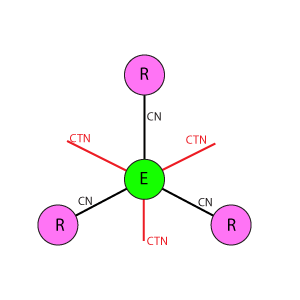
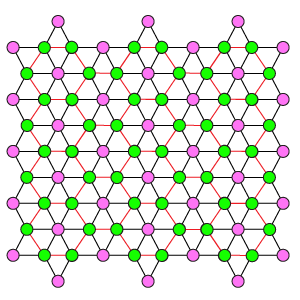
Гексагональная дуплексная схема отличается от DK6-3 более плотной упаковкой рецепторов и большим охватом взаимного тормозного влияния эффекторов. Один эффектор связан с 3 рецепторами, один рецептор связан с 6 эффекторами. Эффекторы имеют взаимное торможение, где каждый тормозит ближайшие 3 соседних.

Дуплексная схема DR4-4

Ортогональная дуплексная схема отличается от DK6-3 и DK3-6 равномерной упаковкой рецепторов и эффекторов, а так же их одинаковым охватом тормозными связями. Один эффектор связан с 4 рецепторами, один рецептор с 4 эффекторами. Эффекторы имеют взаимное латеральное торможение, где каждый эффектор тормозит ближайших 4 соседних.

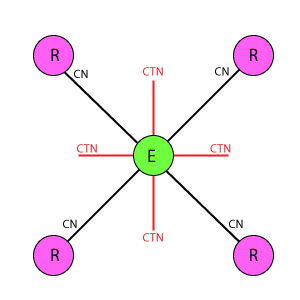
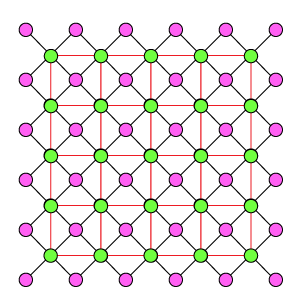
Схема WR9-9

Ортогональная схема из пары одинаковых решеток, расположенных напротив друг друга. Отличается от DK6-3, DK3-6, DR4-4 еще более плотной упаковкой рецепторов и эффекторов, а так же как DR4-4 их одинаковым охватом тормозными связями. Один эффектор связан с 9 рецепторами, один рецептор связан с 9 эффекторами. Эффекторы имеют взаимное латеральное торможение, где каждый эффектор тормозит ближайшие 8 соседних.

В схемотехническом подходе, который используется в статье при изучении принципов работы природной нейросети, предполагается изначально через структуру решетки задание некоторых свойств, определяющих ее поведение – реакцию на раздражитель. Например, в DK6-3 на один эффектор воздействуют 6 рецепторов, а в DK3-6 – наоборот. Это определяет большую рецепторную чувствительность для DK6-3, и соответственно большую эффекторную реакцию для DK3-6. В DR4-4 эти параметры равны – стало быть, обе реакции так же равны. Кроме того, в DK6-3 и DK3-6 рецепторы расположены «волнообразно», по контуру шестигранника, что будет давать некоторое искажение восприятия горизонтальных и вертикальных линий, они будут детектироваться как «дуги». В DR4-4 этого недостатка нет, там наоборот, структура чувствительна в первую очередь для ортогональных линий. WR9-9 отличается от остальных максимальным охватом и как результат более высокой чувствительностью, что проявляется в виде интересных специфических эффектов, о которых будет рассказано ниже. Эти эффекты имеются во всех решетках, но они тем ярче выражены, чем больше охват.

Расчет состояний элементов нейросети методом итераций

В физическом исполнении нейросимулятора не требуется рассчитывать текущие статусы (активен или пассивен) и суммарные веса эффекторов, так как распределение весов и переключение состояний происходит естественным образом благодаря их взаимодействию. В программной реализации это потребует существенных мощностей, которые лавинообразно возрастают при увеличении количества элементов нейросети.

Расчет итогового веса эффектора во всех схемах делается в три этапа:

1. Рассчитывается суммарный вес эффектора без учета взаимного торможения: SumW = Sum(Wr), где Sum(Wr) – сумма весов активных рецепторов, связанных основными связями с текущим эффектором
2. Рассчитывается суммарный вес тормозного влияния на эффектор: SumTr = SumW*Wt
3. Итоговый вес эффектора: Wit = SumW – SumTr

Такой расчет делается последовательно для каждого элемента.

Алгоритм расчета методом итераций

Расчет происходит при изменении статуса хотя бы одного рецептора. Состояния нейронов вычисляется по очереди, в последовательности направления связей. Основная проблема такого алгоритма в том, что идет последовательный опрос элементов с вычислением их суммарного веса и переключения статуса, смотря по тому, стал он выше или ниже порога срабатывания. Но при каждом переключении происходят каскадные изменения весов по всей нейросети, так как элементы связаны взаимными тормозными связями. И может оказаться, что согласно связям, должен измениться статус уже рассчитанного нейрона. Это требует возврата к нему и как результат – для окончательного расчета требуется бесконечный цикл. Проблему можно уменьшить, если делать расчет методом итераций, то есть последовательного приближения, при котором тормозной вес определяется не сразу, а постепенно за несколько шагов итераций, например 10. То есть сначала определяется вес без учета торможения, затем 10 раз пересчитываются итоговые веса всех элементов, увеличивая при каждом шаге тормозное влияние на 1/10 пока оно не достигнет своего полного значения. Такое последовательное приближение позволяет постепенно менять статусы элементов, у которых итоговый суммарный вес (с учетом тормозного влияния) превысит или станет ниже порога срабатывания, а не всем сразу, что сглаживает «перекос переключений» расчета возникающий из-за последовательного перебора. Но полностью решить проблему все равно не удается.

Зависимость поведения нейросети от изменения базовых параметров

Для оценки состояния ячеистой структуры нейросети введем понятие «базовые параметры», изменяя которые можно будет менять ее ответные реакции на внешние раздражители. Такими параметрами будут:

• Up – порог срабатывания нейронов. Он устанавливается общий для всех элементов
• Wt – уровень взаимного торможения между эффекторами. Он так же устанавливается общим для всех
• Ws – вес основных связей между рецепторов и эффектором. Он может быть индивидуальный для каждой связи

Так же введем определения:

• Рецепторный рисунок – группа активных рецепторов фрагмента нейросети
• Эффекторный рисунок – группа эффекторов, активировавшихся рецепторным рисунком
• Уникальная РЭ пара – рецепторный и связанный с ним эффекторный рисунок, уникальный при заданных базовых параметрах нейросети

Из определения видно, что оба типа рисунка всегда идут парой, так как эффекторный рисунок зависит от рецепторного. Это означает, что на определенное раздражение нейросети будет определенный отклик в виде эффекторного рисунка. Однако как будет показано далее, это справедливо лишь при оговоренных базовых параметрах, так как при их изменении нейросеть будет выдавать несколько эффекторных рисунков на один и тот же рецепторный. Поэтому вводится понятие не просто пары, а уникальной – чтобы учитывать только те эффекторные рисунки, которые строго одинаковы при заданных рецепторном рисунке и базовых параметрах нейросети. Все прочие будут считаться случайно-хаотическими, вызванные какими-то  погрешностями расчета.

В природной нейросети тормозное влияние осуществляется при помощи пары вставочных тормозных нейронов, отличающихся от обычных тем, что они при возбуждении передают связанному с ними эффектору не активирующий сигнал, а тормозной. То есть полноценная схема связей, например, для решетки DR4-4 должна выглядеть так (сделано в конструкторе нейросхем):

Базовый элемент схемы DR4-4

• Ei – эффектор
• Ri – рецептор
• Ti – тормозной нейрон

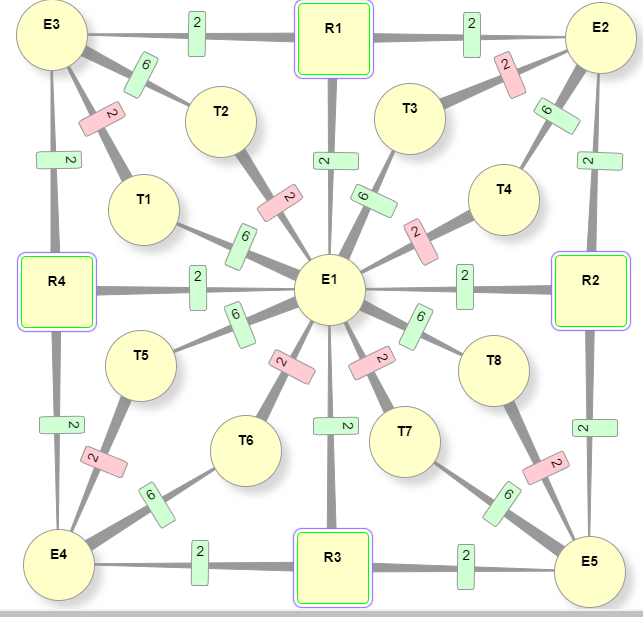
Линии связей острием показывают свое направление. Прямоугольники на них это синапсы, цифра внутри показывает текущий вес связи, которая может быть двух видов: тормозная (красный цвет) и основная (зеленый). Рецепторы воздействуют на эффекторы с весом =2, что означает в данной схеме логику связей И, потому что для активации эффекторов нужно как минимум 3 рецептора, чтобы превысить порог срабатывания =5. В тоже время эффекторы активируют тормозные нейроны, которые взаимно тормозят активацию пары связанных с их помощью эффекторов. Итогом станет специфическое реагирование нейросети, зависящее от порядка активации рецепторов и значения ее базовых параметров.

Но в целях упрощения визуального представления, в моделях вместо пары тормозных нейронов будет отражаться просто линия тормозной связи, обладающей тем же свойством взаимно тормозить связанные через нее элементы. Другая особенность ячеистых схем построения нейросети в данных нейросимуляторах – одинаковый вес у связанных с рецептором эффекторов. Дело в том, что забегая вперед и размышляя о самообучении таких решеток, зададимся вопросом: какие веса могут теоретически установится в ячеистых схемах, где один рецептор передает возбуждение нескольким связанным с ним эффекторам? Тут возможны две ситуации:

1. Все нейроны слоя начинают самообучение примерно одновременно и имеют одинаковые параметры. Тогда вес связей при самообучении у них будет так же расти с одинаковой скоростью. Чтобы вес был разный, что то, например взаимное торможение, должно влиять на скорость наращивания веса синапсами. Из этого вытекает, что тормозные нейроны должны созреть раньше основных и успеть установить с ними тормозные связи до начала обучения. Это в свою очередь ставит вопрос как тормозные нейроны протягивают связи: сумбурно-хаотично, ориентируясь на пейсмейкерную активность или как то еще? Может последовательность созревания разных типов нейронов заложена в геноме? И как вообще тормозной нейрон влияет на активность синапса обычного нейрона, на который он воздействует?
2. Нейроны слоя созревают для самообучения не одновременно. Это значит, что к одному рецептору подключаются по мере созревания несколько эффекторов, и при каждом образовании новой связи с новым эффектором активность рецептора может быть разной, отчего и веса связей от одного рецептора получаются различными.

В данном симуляторе мы рассматриваем уравновешенные ячеистые решетки как наиболее простой вариант для практической реализации прототипа, где все нейроны слоя одновременно созрели и готовы для самообучения. Это так же  делается с целью определить, к чему приведет такое упрощение. Далее рассмотрим поведение разных типов решеток и попробуем его объяснить.

Модель гексагональной дуплексной схемы DK6-3

Пример симулятора поведения решетки DK6-3 при расчете методом итераций.

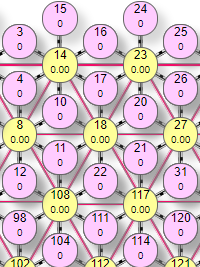Матрица выполнена в виде ячеистой структуры по типу шестигранника, где в центре находится эффектор (на рисунке это элементы с номерами 14,23, 8, 18, 27, 108, 117). Вокруг него веером расположены рецепторы. В данной схеме каждый элемент имеет 2 числовых значения внутри. Более крупная цифра, расположенная выше – порядковый номер элемента в сети. Например, цифры 10, 11, 12 и т.д. Более мелкая цифра ниже: Для эффектора – показывает суммарный вес, полученный от рецепторов Для рецептора – вес, передаваемый связанным с ним эффекторам Имитация воздействия на рецептор производится простым кликом по кружку, после чего он меняет цвет и вес связи, передаваемый связанному с ним эффектору. При клике левой кнопкой вес увеличивается от 0,1 до 0,9 и цвет становится более насыщенным, при клике правой – вес уменьшается и цвет становится более тусклым.

Так имитируется установка веса на синапсе нейрона-эффектора. Чтобы сразу задать максимальный вес рецептора 0,9 нужно сделать первый клик (по рецептору с весом 0) левой кнопкой. Если по рецептору с весом 0,9 кликнуть правой – его вес обнулится. Одновременно с изменением веса рецепторов меняется значение суммарного веса у эффектора.

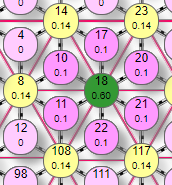Состояние элементов на рисунке показано при настройках сети: Порог = 0,4 Вес тормозных связей = 0,1 На рисунке таким образом были активированы 6 рецепторов (№10, 11, 17, 20, 21, 22) с весом передаваемого возбуждения 0,1. Они в свою очередь активировали эффектор (элемент 18) передав ему суммарный вес 0,6. По текущим настройкам сети порог срабатывания эффектора 0,4.

Поэтому, так как переданный ему от рецепторов суммарный вес превысил порог – он активировался, что демонстрируется изменением его цвета. Кроме того, на рисунке видны линии связи 2 типов:

• Основная связь – между рецепторами и эффектором. По ней передается уровень сигнала от рецептора к эффектору с заданным весом.
• Тормозная связь – только между эффекторами. По ней передается взаимное торможение, но только от активных эффекторов.

У симулятора есть несколько настроек, позволяющих имитировать изменения параметров элементов сети. Они расположены ниже и представляют собой поле, в которое можно вводить числовое значение параметра и ползунок, перемещая который можно динамически менять значение того же параметра. Крайние справа – 2 графических настройки в виде флажков. Рассмотрим настройки более подробно:

• Порог срабатывания для всех нейронов – поле и ползунок. Задает общий для всех эффекторов порог срабатывания. Это означает, что как только суммарный вес эффектора превысит величину порога, он активируется и начнет оказывать тормозное влияние на связанные с ним тормозными связями соседние эффекторы.
• Коэффициент увеличения веса – поле и ползунок. Задают общий для всех основных весов коэффициент усиления, имитирующий уровень воздействия на активные рецепторы.
• Вес для всех тормозных связей – устанавливает общий для всех эффекторов тормозной вес. Тормозное влияние передается только от активного эффектора и рассчитывается по формуле:

Суммарный вес активного эффектора * вес тормозной связи

В данном случае от эффектора передается тормозное влияние величиной: 0,6*0,1=0,06 условных единиц. И поступает оно на каждый их шести эффекторов связанных с активным тормозными связями (элементы 14, 23, 27, 117, 108, 8). Но на эти же эффекторы поступили сигналы от активных рецепторов с величиной 0,1. При этом например на эффектор 14 поступили сигналы от рецепторов 10 и 17, что в подняло его суммарный вес до: 0,1*2=0,2. В итоге, два типа воздействия на эффектор 14 установили его итоговый вес как суммарный вес от рецепторов за минусом тормозного влияния от активных эффекторов, имеющих с ним связи (в данном примере только один эффектор на него влияет (№18): 0,2-0,06=0,14. Аналогичным образом устанавливаются итоговые веса остальных эффекторов, на которые поступило активно/тормозное влияние элементов нейросети.

• Показать линии связей – нажатие флажков отображает линии связей элементов, отжатие – скрывает.
• Загрузить рисунок – поле со списком, позволяющее загрузить готовый рецепторный рисунок. Служит альтернативой ручной активации рецепторов.

Интерактивный график суммарных весов эффекторов

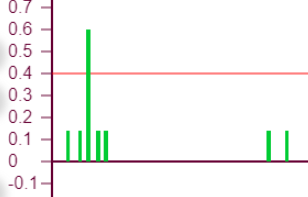Справа от модели нейросети расположен интерактивный график, где показаны значения весов эффекторов. По вертикали отражаются веса (вверх – положительные, вниз - отрицательные), по горизонтали – номера элементов сети. Значение весов показаны в виде вертикальных линий, длина которых соответствует весу. Горизонтальная линия пересекающая значения весов с надписью «Порог» показывает текущее значение порога срабатывания эффекторов. Ее положение связано со значение в поле «Порог срабатывания для всех нейронов» или ползунка рядом с ним. График позволяет более наглядно демонстрировать поведение сети при активации рецепторов или изменении параметров.

Теперь рассмотрим простейшие примитивы и примеры расчета весов.

1 шаг – вес без учета взаимного торможения:

Три рецептора 22, 21, 31 передают свой потенциал на связанные с ними эффекторы с коээф. передачи 0,2 образуя суммарный вес на эффекторах (без учета торможения):

• №108 - получает воздействие от рецептора 22: 0,2
• №17 – получает воздействие от рецепторов 22, 21, 31: (0,2+0,2+0,2) =0,6
• №18 - получает воздействие от рецепторов 22, 21: (0,2+0,2) =0,4
• №27 - получает воздействие от рецепторов 21, 31: (0,2+0,2) =0,4
• №126 - получает воздействие от рецептора 31: 0,2

2 шаг – расчет тормозного воздействия

Так как активировался только один эффектор №117, то только он и притормаживает связанные с ним тормозными связями эффекторы № 108, 18, 27, 126,  121, 112. То есть эти эффекторы получают двойное воздействие: активирующее от активных рецепторов №22, 21, 31 и тормозное от эффектора №117. Последнее рассчитывается так: 0,6*0,2=0,012

3 шаг – расчет итогового веса

Теперь вычитаем из суммарного веса без учета торможения тормозной вес – и так для каждого эффектора, получившего активно/тормозное воздействие:

• №108: 0,2-0,012=0,08
• №18: 0,4-0,012=0,28
• №27: 0,4-0,012=0,28
• №126: 0,2-0,012=0,08
• №121: 0-0,012=-0,012
• №112: 0-0,012=0,012

Как видим, эффекторы №121, 112 получили только тормозное воздействие, в итоге их вес стал отрицательным. Физический смысл этого – эффектор изначально приторможен. На графике состояние весов показано более наглядно. Две вертикальных полоски слева со значением 0,28 отражают положительные веса №18, 27. Самая большая полоска справа со значением 0,6 – активный эффектор. Обратим внимание – его вес вышел за порог срабатывания (горизонтальная линия порога с уровнем 0,4) – поэтому он активировался и начал оказывать тормозное влияния на связанные с ним эффекторы. Теперь рассмотрим более сложный примитив.

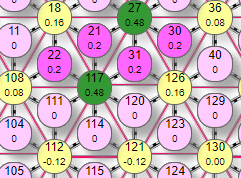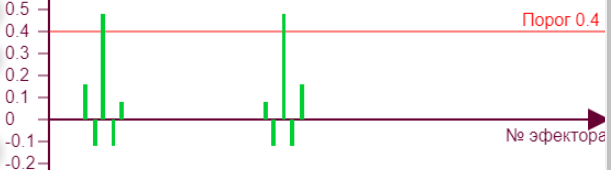Здесь активны уже 4 рецептора №22, 21, 31, 30 которые передали веса на связанные с ними эффекторы 

№117, 27. И теперь они начинают взаимно тормозить друг друга, передавая соседу тормозное влияние 0,6*0,2=0,12. Поэтому их итоговый вес: 0,6-0,12=0,48. Кроме того, эффектор №18 получил кроме активирующего влиянии от рецепторов №22, 21 еще и два тормозных влияния от активных эффекторов №117, 27. Поэтому его итоговый вес стал: (0,2+0,2)-(0,6+0,6)*0,2=0,16. Аналогично определился вес эффектора №126 – он также получил двойное активно/тормозное воздействие. На графике теперь мы видим два превышения порога срабатывания – это активные эффекторы. Добавим еще один рецептор в примитив и посмотрим, как изменится состояние сети.

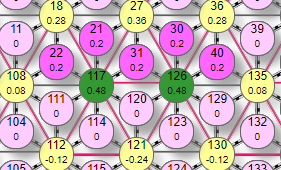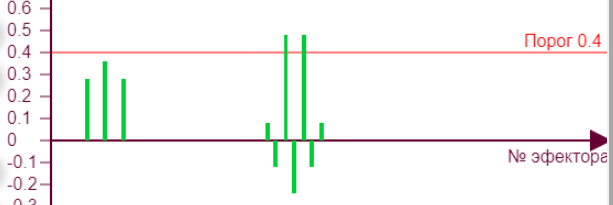Тут схема распределения весов становится интересной тем, что выключился активный эффектор, который без взаимного торможения оставался бы активным. Его суммарный вес за счет торможения от двух соседних стал ниже порога. То есть не будь торможения, веса эффекторов №117, 27, 126 были бы все по 0,6. Но так как теперь эта тройка начала тормозить друг друга, то их веса соответственно уменьшились на величину торможения, в данном случае 0,12. Поэтому веса эффекторов № 117, 126 уменьшились на эту величину. И оба они воздействуют на эффектор №27, уменьшая его вес на 0,12*2=0,24, устанавливая его итоговый вес: 0,6-0,24=0,36. Однако, возникает вопрос: ведь то же самое можно сказать и про другие эффекторы. № 117 тормозят №27, 126, а №126 соответственно притормаживают №117, 27. Строго говоря, любой из них мог оказаться выключенным, но выключился именно №27. То, что именно ему уготовано быть отключенным легко проверить включая/отключая в любой последовательности эти пять включенных рецепторов – при активации всех пяти всегда именно он окажется выключенным. Но в данном случае, так как суммарные веса эффекторов получились вблизи порога срабатывания, неоднозначность ситуации решилась в виде выключения №27 потому, что в алгоритме расчета весов симулятора последовательно обходятся все эффекторы в порядке возрастания их номеров. Поэтому для №27 вес рассчитывается раньше всех – и получается равным 0,36, что ниже порога, после чего он тут же выключается и перестает учитываться в расчете остальных двух весов активных эффекторов. Метод итераций при самом мелком шаге все равно будет приводить к такому результату, поэтому увеличение числа итераций ничего не решит.

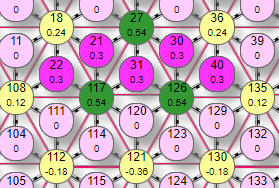В реальной нейросети тоже самое произойдет из за некоторой нестабильности параметров нейронов и случайных флуктуаций. Только там уже нельзя будет определенно сказать, какой из эффекторов окажется выключенным. Убедиться, что проблема именно в неустойчивом состоянии возле порога срабатывания можно задав веса всем пяти рецепторам 0,3 – и тогда получим уверенное равновесное состояние.

Но как уже говорилось, ситуация с одинаковыми весами от рецепторов не типична для реальной нейросети, поэтому выключение №27 будет уже строго определено например при таком раскладе весов:

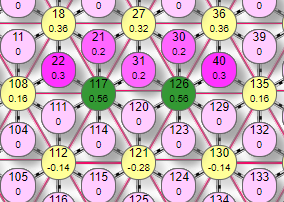Здесь уже виден эффект контрастирования – выделения более нагруженных весами эффекторов. В данном случае №117, 126 получили веса 0,3+0,2+0,2=0,7 а №27 – 0,2+0,2+0,2=0,6. Два более сильных эффектора тормозной связью 0,2 задавили более слабый №27, и взаимно понизили веса друг друга.

Добавим еще один рецептор. Здесь снова виден эффект контрастирования, но с особенностью, прежде не проявлявшейся: эффекторы №36, 117 показывают свой полный суммарный вес 0,6, как будто не испытывают взаимного торможения.

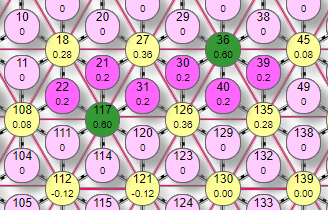Так и есть – если посмотреть на линии тормозных связей, то видно, что эти два эффектора не связаны между собой, поэтому и не тормозят друг друга. Зато они успешно притормозили два других - №27, 126 до уровня меньше порога, отчего они выключились и прекратили притормаживать №36, 117. Поэтому оставшиеся эффекторы, вернули свой начальный вес. Это можно сравнить с качелями, где при нагрузке одной из перекладин, она падает вниз, а другая синхронно с ней летит вверх. Буквально так и произошло с этими парами эффекторов.

Теперь рассмотрим практическое применение в схемотехнике нейросети симулятора эффекта взаимного торможения: как и для чего он используется. То, что при этом отдельные эффекторы теряют в весе вплоть до выключения – думаю уже очевидно, но что это дает например для распознавания образов в простейшей децентраизованной нейросети, где нет еще специализированных модулей формирования примитивов, или говоря иначе, что можно в плане распознавания образов сделать уже на первых слоях?

Примеры использования взаимного торможения в нейросети

Как видно из описания схемы симулятора, на элементы нейросети воздействуют два фактора: активация рецепторов и тормозное влияние активировавшихся эффекторов. Это в итоге приводит к сложной реакции нейросети с различными эффектами, имеющими принципиальное значение при распознавании образов.

Контрастирование примитива

Выключение самых слабо нагруженных эффекторов означает, что остаются только самые нагруженные и тем самым происходит фильтрация слабых сигналов. Это как бы самоочевидно. Но вот то, что взаимное торможение так же позволяет делать прямо противоположное, а именно выделять даже самые слабые сигналы, на первый взгляд кажется противоречивым. Ведь торможение судя по названию должно тормозить, а не усиливать. Но посмотрим на рисунок. На первом мы видим 5 активных эффекторов, 4 в группе и один отдельный. Это при уровне торможения 0,1. На втором рисунке мы видим только 2 включенных эффектора: один из группы и тот же отдельно от них стоящий №215. Это уже при максимальном уровне торможения 1. Взаимным торможением эффекторов в группе из них остался только один самый нагруженный, но так же и отдельно стоящий, не связанный с группой тормозными связями и потому не получивший тормозного влияния. При этом его вес может лишь слегка превышать уровень порога. В итоге получается, что взаимное торможение как бы выделило этот слабый эффектор среди группы более сильных потому, что большая часть из группы была просто выключена торможением. То есть контрастирование через взаимное торможение не означает усиление сильно нагруженных или ослабление слабо нагруженных эффекторов, это частные случаи эффекта, а выделение наименее заторможенных. Это может быть как наиболее сильный эффектор, а потому и меньше всего потерявший в весе, но также и просто одиночный, не связанный тормозными связями с текущими активными эффекторами.

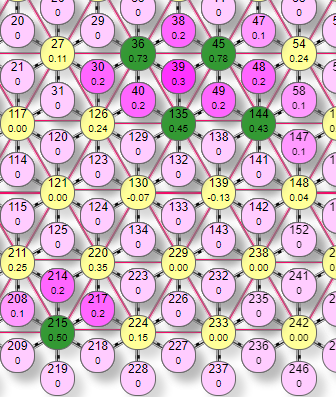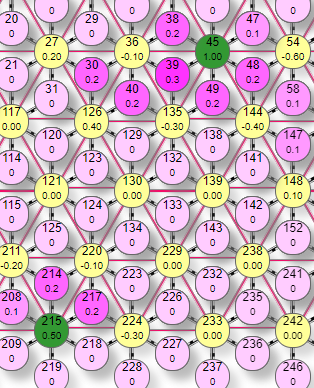Этот эффект мы можем наблюдать когда  небольшое почесывание внезапно становится сильным зудом в виде точечного раздражения, словно укол иголкой. Таким образом могут выделяться даже очень слабые сигналы. Но если говорить о контрастировании в общем смысле как выделении признака, то это хорошо видно по следующим трем рисункам.

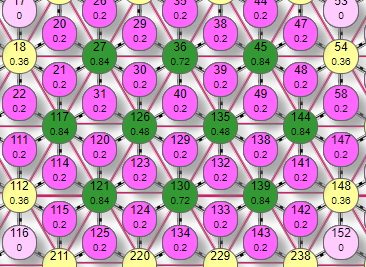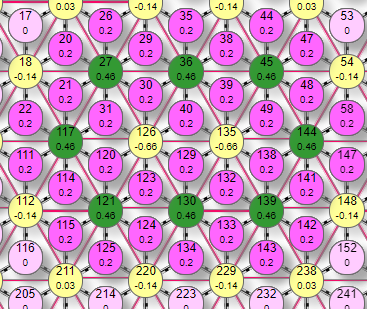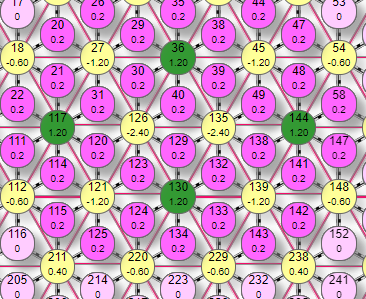На первом видна область активных эффекторов, включенных областью активных рецепторов. Это при уровне торможения 0,1. Если увеличить его до 0,3 то останутся активными только эффекторы по границе области. Если увеличить его до 0,4 то активны стали только 4, которые к тому же вернули себе исходный вес. Дальнейшее увеличение уровня торможения не изменит эффекторный рисунок, так как все эффекторы, имеющие связи с этими 4 активными оказались выключенными ими же и не могут на них влиять. В итоге, в первом случае мы получили при детектировании рецепторного рисунка типа «пятно» аналогичный эффекторный рисунок в виде «пятна», при увеличении уровня торможения до 0,3 – границу контура, при увеличении до 0,4 – опорные точки примитива.

Разбиение сложного примитива на более простые

Если стоит задача сравнить сложные примитивы, то сначала нужно выделить у них какие то признаки, что означает разбиение примитива на более простые, например разбить многогранник на отдельные линии, а длинные линии на более короткие. Это так же делается при помощи взаимного торможения, которое было рассмотрено выше на примерах, когда выключались эффекторы. Получалось как бы разбиение отрезка на пунктирную линию, а фигуры на отрезки, которые детектируются уже отдельными эффекторами. То есть задача в том, чтобы воспринимать фигуру не как одно целое, а в виде отдельных частей, которые потом можно группировать, сравнивать – что означает продолжение анализа примитива на других слоях. Хотя само по себе разбиение предопределено уже тем, что эффекторы в симуляторе охватывают только по 6 ближайших к ним рецепторов. А это не позволит детектировать одним эффектором большую фигуру – она автоматически будет распознаваться группой эффекторов. Но такое разбиение не получится модулировать (регулировать, изменять) каким то внешним параметром, например параметрами гомеостаза – и переключать контексты восприятия. Поэтому разбиение обусловленное только схемой соединения (охвата) эффекторов и рецепторов имеет мало практического смысла.

Конфигурирование нейросети

До сих пор мы рассматривали изменения сети при постоянных значениях ее параметров, только меняя образы (примитивы) на рецепторном поле. Теперь посмотрим, что будет происходить при детектировании одного и того же образа, но при изменении параметров (порога срабатывания эффекторов и уровня тормозного влияния). В описании примера контрастирования «пятна» на 3 снимках было видно, что при увеличении торможения эффекторный рисунок меняется несколько раз. Он так же будет меняться и при изменении уровня порога. А так же при изменении обоих параметров. То есть меняя параметры сети получаем возможность создания серии эффекторных рисунков при детектировании одного рецепторного. Можно сказать, что мы таким образом создаем конфигурации эффекторного рисунка, различные варианты отклика сети на один раздражитель при разных условиях.

Представим, что есть еще одна сеть, «следящая» за параметрами гомеостаза, выходные сигналы которой способны воздействовать на параметры первого слоя. И тогда мы получаем простейшую модель смены контекста восприятия, что означает смену моделей поведения, в зависимости от текущих параметров гомеостаза. Можно предположить, что именно так регулировалась нервная система у простых древних организмов, пока не возникли более сложные механизмы переключения моделей и она осталась в наследие и продолжает работать в первичных зонах и задает первичную корректировку при детектировании образов.

Резюмируем вышесказанное:

Ячеистая компоновка элементов нейросети при изменении ее базовых параметров приводит к генерации серии эффекторных рисунков, что позволяет контрастировать, дефрагментировать и конфигурировать детектируемые примитивы. Это свойство на ранних этапах эволюции нервной системы вполне могло служить для простейшей схемы гомеостатической регулировки эффекторной активности и предположительно могло сохраниться в первичных зонах. Для уточнения нужны дополнительные исследования.

Модель ортогональной дуплексной схемы DK4-4

Пример симулятора поведения решетки DK4-4 при расчете методом итераций.

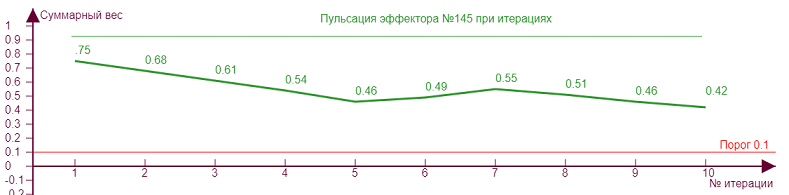Матрица выполнена в виде ортогональной дуплексной решетки, где в его центре находится эффектор (на рисунке это элементы с номерами 38,48, 60, 70, 50, 72, 40,62). Вокруг эффектора ортогонально расположены 4 рецептора. В данной схеме каждый элемент имеет 2 числовых значения внутри Более крупная цифра, расположенная выше – порядковый номер элемента в сети. Например, цифры 37, 38, 39 и т.д. Более мелкая цифра ниже: Для эффектора – показывает суммарный вес, полученный от рецепторов Для рецептора – вес, передаваемый связанным с ним эффекторам

Так как решетка ортогональная, то для большей плотности упаковки элементы выполнены в виде квадратов. Имитация воздействия на рецептор производится простым кликом по нему, после чего он меняет цвет и вес связи, передаваемый связанным с ним эффекторам. При клике левой кнопкой вес увеличивается от 0,1 до 0,9 и цвет становится более насыщенным, при клике правой – вес уменьшается и цвет становится более тусклым. Так имитируется установка веса на синапсе нейрона-эффектора. Чтобы сразу задать максимальный вес рецептора 0,9 нужно сделать первый клик (по рецептору с весом 0) левой кнопкой. Если по рецептору с весом 0,9 кликнуть правой – его вес обнулится. Одновременно с изменением веса рецепторов меняется значение суммарного веса у эффектора.

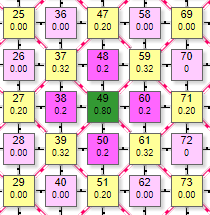Состояние элементов на рисунке показано при настройках сети: Порог=0,4 Вес тормозных связей=0,1 На рисунке таким образом были активированы 4 рецептора (№38, 48, 50, 60) с весом передаваемого возбуждения 0,2. Они в свою очередь активировали эффектор (элемент 49) передав ему суммарный вес 0,8. По текущим настройкам сети порог срабатывания эффектора 0,4. Поэтому, так как переданный ему от рецепторов суммарный вес превысил порог – он активировался, что демонстрируется изменением его цвета. Кроме того, на рисунке видны линии связи 2 типов: Основная связь – между рецепторами и эффектором. По ней передается уровень сигнала от рецептора к эффектору с заданным весом. Тормозная связь – только между эффекторами. По ней передается взаимное торможение, но только от активных эффекторов.

У симулятора есть несколько настроек, позволяющих имитировать изменения параметров элементов сети. Они расположены ниже и представляют собой поле, в которое можно вводить числовое значение параметра и ползунок, перемещая который можно динамически менять значение того же параметра. Они аналогичны настройкам ранее рассмотренной гексагональной решетки:

• Рецепторный рисунок - поле со списком, позволяющее загрузить готовый рецепторный рисунок. Служит альтернативой ручной активации рецепторов.
• Тип отображения - поле со списком, позволяющее переключать симулятор из дуплексного в двойной режим отображения матриц.
• Порог срабатывания эффекторов – поле и ползунок. Задает общий для всех эффекторов порог срабатывания. Это означает, что как только суммарный вес эффектора превысит величину порога, он активируется и начнет оказывать тормозное влияние на связанные с ним тормозными связями соседние эффекторы.
• Вес тормозных связей – устанавливает общий для всех эффекторов тормозной вес. Тормозное влияние передается только от активного эффектора и рассчитывается по формуле:

Суммарный вес активного эффектора * вес тормозной связи

В данном случае от эффектора передается тормозное влияние величиной: 0,8*0,1=0,08 условных единиц. И поступает оно на каждый их четырех эффекторов связанных с активным тормозными связями (элементы 37, 39, 59, 61). Но на эти же эффекторы поступили сигналы от активных рецепторов с величиной 0,2. При этом например на эффектор 37 поступили сигналы от рецепторов 38 и 48, что в подняло его суммарный вес до: 0,2*2=0,4. В итоге, два типа воздействия на эффектор 37 установили его итоговый вес как суммарный вес от рецепторов за минусом тормозного влияния от активных эффекторов, имеющих с ним связи (в данном примере только один эффектор на него влияет (№18): 0,4-0,08=0,32. Аналогичным образом устанавливаются итоговые веса остальных эффекторов, на которые поступило активно/тормозное влияние элементов нейросети.

Пример расчета весов эффекторов аналогичен рассмотренному выше для гексагональной решетки, поэтому повторять его здесь не будем. Отметим лишь особенности ортогональной решетки при детектировании ей простейших примитивов. Для этого воспользуемся списком «Рецепторный рисунок» и последовательно выберем из него несколько примитивов и посмотрим как будет меняться рецепторный рисунок при разных значениях тормозного воздействия.

Горизонтальная линия

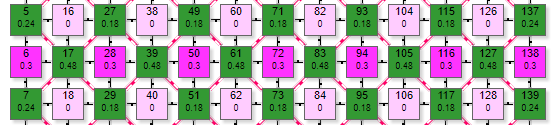Для такого рисунка нужно задать параметры: Вес рецептора – 0,3 Порог – 0,1 Торможение – 0,1

Так как торможение и порог минимальны, то активны все связанные с рецептором эффекторы, хотя все же итоговый вес у них распределился не равномерно, смотря по тому, кто больше/меньше оказался заторможен

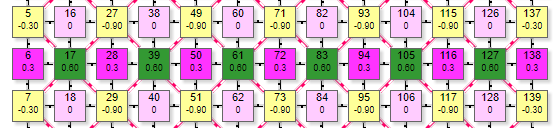Для такого рисунка нужно задать параметры: Вес рецептора – 0,3 Порог – 0,1 Торможение – 1

Торможение максимально, что привело к полному гашению все связанных эффекторов, оставив лишь центральный, как наиболее нагруженный рецепторным весом. Лишившись тормозного влияния соседей он показывает свой полный вес, как если бы никакого торможения не было. Здесь хорошо проявлен эффект контрастирования примитива по сравнению с предыдущим вариантом, где линия максимально «толстая» - здесь она наоборот – максимально «тонкая».

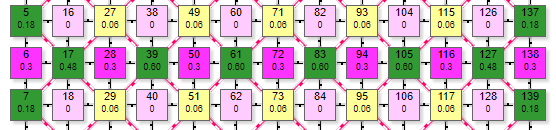Для такого рисунка нужно задать параметры: Вес рецептора – 0,3 Порог – 0,1 Торможение – 0,2

Здесь мы видим утолщение примитива на концах, или утончение по центру. Такой вариант эффекторного рисунка подойдет для детектирования пары опорных точек примитива, так как на втором слое эффекторы, расположенные физически рядом с ними получат больший итоговый вес, что позволит используя тоже самое контрастирование выделить их среди прочих как отдельную пару. То есть на втором слое можно при определенных параметрах получить эффекторный рисунок в виде 2 отдельных эффекторов, физически расположенных на концах отрезка.

Таким образом мы получаем три конфигурации ответного эффекторного рисунка при разных параметрах нейросети. Это означает, что если создать связь между параметрами решетки и каким то внутренним параметром, например параметром гомеостаза, то на один и тот же раздражитель при разных внутренних условиях нейросеть будет реагировать по разному. Выше уже высказывалось предположение, что у древних организмов с нестабильными параметрам нейросети, такое свойство нейросети могло использоваться как примитивная регулировка рефлекторной реакции гомеостатической значимостью. Например голодная особь видит «толстый отрезок», сытая «тонкий», встревоженная «опорный точки» и т. д. От каждого такого эффекторного рисунка могла выстроиться и эволюционно закрепиться своя рефлекторная цепочка реагирования.

Крест

Для такого рисунка нужно задать параметры: Вес рецептора – 0,3 Порог – 0,1 Торможение – 0,1 Здесь мы видим максимальное «утолщение» эффекторного рисунка как и в предыдущем варианте при минимальном торможении и пороге.

Для такого рисунка нужно задать параметры: Вес рецептора – 0,3 Порог – 0,1 Торможение – 1 Здесь мы видим максимальное «утончение» эффекторного рисунка. Но интересно тут другое: если начать плавно двигать ползунок с уровнем торможения в сторону увеличения, то прежде чем прийти к данному варианту, решетка выдаст целую серию конфигураций рисунков, причем некоторые из них будут повторяться при разных значениях торможения, что будет отображаться в виде «генерации колебаний» - переключения между парами одинаковых рисунков.

Это происходит из за большего охвата тормозными связями соседних эффекторов при детектировании наклонных линий, что приводит к неоднозначным состояниям. В итоге возникают пары эффекторов, которые могут равновероятно быть активными и пассивными. В реальной нейросети случайная флуктуация привела бы к переключению в одно из состояний, что означает не определенность результата детектирования. То есть решетка в таком состоянии не способна выдавать уникальную пару РЭ рисунков, вместо этого она генерирует несколько  случайных пар, что означает не однозначность детектирования. Для ортогональной решетки такая неоднозначность возникла при попытке детектировать наклонные линии, в отличие от ортогональных прямых, где было всего три типа рисунка. Следовательно, ортогональная решетка наиболее точно детектирует ортогональные примитивы. Проверим это на примере квадрата.

Квадрат

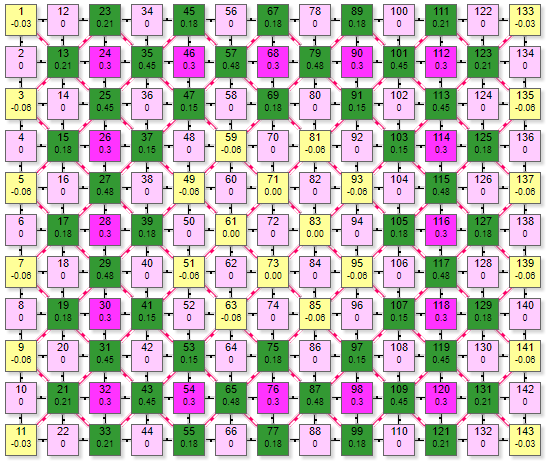	Для такого рисунка нужно задать параметры: Вес рецептора – 0,3 Порог – 0,1 Торможение – 0,1 Здесь мы по прежнему видим максимальное «утолщение» эффекторного рисунка как и в предыдущих вариантах при минимальном торможении и пороге.
	Для такого рисунка нужно задать параметры: Вес рецептора – 0,3 Порог – 0,1 Торможение – 0,2 Здесь мы видим максимальное «утончение» эффекторного рисунка. При этом максимально обозначились опорные точки примитива по углам квадрата в виде 4 активных эффекторов. При уровне торможения 0,3 они сократятся до 3, при торможении 0,4 до 2.
	Для такого рисунка нужно задать параметры: Вес рецептора – 0,3 Порог – 0,1 Торможение – 1 При максимальном торможении итоговый рисунок распался на отдельные отрезки разной «длины». Слово длина в скобках потому, что такое понятие так как мы его понимаем в виде кол-во единиц измерения на этом уровне детектирования еще не существует. Здесь просто фиксируется активность эффекторов, в данном случае отдельных групп «горизонтальных» и «вертикальных» линий.

При этом понятие горизонтальность/вертикальность так же некорректно на этом уровне. Правильнее назвать их просто группа 1 и группа 2, так как единственное, что может определиться на втором слое при детектировании этих отрезков – их отличие одного от другого. Собственно это как и раз и важно, так как произошло разбиение сложного примитива на более простые, что позволит в дальнейшем на следующих уровнях определить такие понятия как «свойство объекта»: если примитивы определятся как «ортогональные линии» – значит это «прямоугольник», если они «равной длины» - значит это «квадрат». И предварительная «подготовка данных» для таких оценок происходит уже в первых слоях распознавателя.

Резюмируем вышесказанное:

Эксперименты с ортогональной компоновкой подтвердили предыдущий вывод: ячеистая компоновка элементов нейросети при изменении ее базовых параметров приводит к генерации серии эффекторных рисунков, что позволяет контрастировать, дефрагментировать и конфигурировать детектируемые примитивы – подготавливать данные для последующей обработки. Добавилось еще одно наблюдение: ортогональная решетка более чувствительна к детектированию ортогональных примитивов, а наклонные линии приводят к неоднозначности реагирования.

Модель ортогональной схемы WR9-9

Пример симулятора поведения решетки WR9-9 при расчете методом итераций.

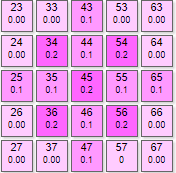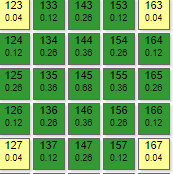Модель выполнена в виде двух отдельных ортогональных решеток рецепторов и эффекторов. Выполнить ее по дуплексной схеме не представляется возможным, так как охват при такой схеме наибольший: с 1 рецептором связаны 9 эффекторов, с 1 эффектором 9 рецепторов. По причине излишнего загромождения графикой в этом симуляторе условно не показаны линии связей.

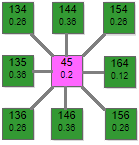
Схема представляет собой две параллельно расположенных решетки: рецепторную и эффекторную над ней. Схема связей между ними показана на примере рецептора 45 и эффекторов 134,135,136,146,

156,164,154,144,134. Эффектор 145 условно не показан, так как он расположен под рецептором 45. Таким же образом соединены и остальные элементы двух решеток. Аналогична схема тормозных связей в эффекторной решетке, только там уже один эффектор связан с 8 соседними.

Рассмотрим элементы управления параметрами симулятора, в котором добавлены новые элементы.

• Рецепторный рисунок - поле со списком, позволяющее загрузить готовый рецепторный рисунок. Служит альтернативой ручной активации рецепторов.
• № эффектора - поле со списком, позволяющее выбирать эффектор для наблюдения изменения его итогового веса при итерациях.
• Порог срабатывания эффекторов – поле и ползунок. Задает общий для всех эффекторов порог срабатывания. Это означает, что как только суммарный вес эффектора превысит величину порога, он активируется и начнет оказывать тормозное влияние на связанные с ним тормозными связями соседние эффекторы.
• Вес тормозных связей – устанавливает общий для всех эффекторов тормозной вес. Тормозное влияние передается только от активного эффектора и рассчитывается так же как и ранее.

В интерактивном графике добавлена линия уровня суммарного веса выбранного эффектора при итерациях расчета. Это сделано с целью изучить, как происходит установка итогового веса эффектора с учетом взаимного торможения его соседей. Из 2 предыдущих схем стала очевидна прямая зависимость между охватом связями элементов и количеством конфигураций эффекторных рисунков при изменении базовых параметров: чем больше охват – тем больше конфигураций, включая не однозначные состояния, приводящие к «генерации колебаний» эффекторных рисунков. В этой схеме это проявляется в еще большей степени, в чем можно убедиться, перемещая ползунки порога и уровня торможения. Так же как и ранее максимальное количество вариантов реагирования будет при минимальном пороге. Формулы расчета весов аналогичны предыдущим примерам. Здесь мы рассмотрим такое явление как «колебания» суммарного веса эффектора при увеличении тормозного влияния. Данный эффект происходит за короткий отрезок времени и как бы показывает в «замедленной съемке», что происходит с эффектором в момент его активации. Основанием для того, что это не погрешность расчета служит то, что итерации означают постепенное увеличение тормозного влияния за несколько шагов, что в реальности симулирует некоторую инертность нейрона. Порядок активации нейрона мне представляется следующим образом:

1. Получивший заряд активации от связанных с ним рецепторов нейрон активируется. Происходит быстрый рост возбуждения.
2. Одновременно с этим активируются и соседние нейроны, ведь они тоже имеют связи с этими рецепторами. Но так как они охвачены тормозными связями, то при активации включается взаимный процесс торможения тем больший, чем сильнее тормозное влияние.
3. Результатом торможения будет спад активности связанных тормозными связями нейронов – уменьшение их суммарного веса. Что в свою очередь приведет к уменьшению тормозного влияния.

В этой схеме присутствует обратная связь, провоцирующая автоколебания, что должно отразиться на графике роста веса нейрона при активации в виде ломанной кривой, которая изгибается тем сильнее, чем больше тормозное влияние. Теперь посмотрим, что происходит в симуляторе.

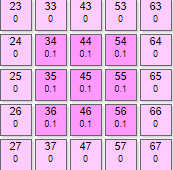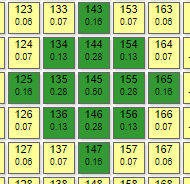		Для такого рисунка нужно задать параметры: Вес рецепторов – 0,1 Порог – 0,1 Торможение – 0,1 Здесь при минимальных параметрах нейросети видим почти ровную кривую спада уровня возбуждения при итерациях. Сначала эффектор №145 получил максимальный вес, потом тормозное влияние соседей плавно опустило его итогового значения.

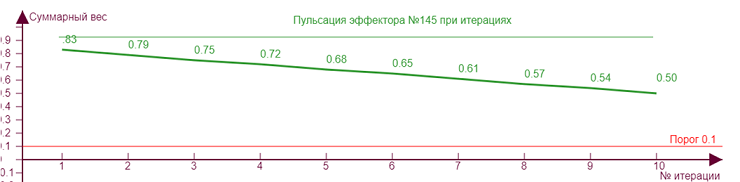Если начнем двигать ползунок уровня торможения, то получим серию различных эффекторных рисунков, так как из за все возрастающего тормозного влияния эффекторы начнут попеременно включаться/выключаться, изменяя тем самым свое тормозное влияние на исследуемый эффектор №145, что вызовет аналогичные скачки роста уровня активности на нем. Чем больше тормозное влияние, тем сильнее изломы кривой.

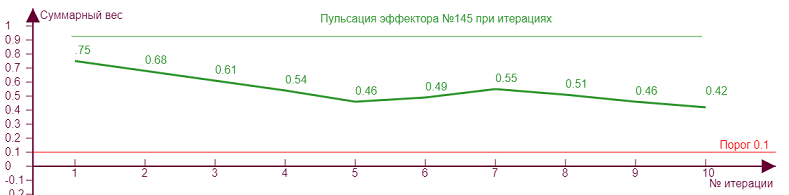	Вес рецепторов – 0,1 Порог – 0,1 Торможение – 0,2
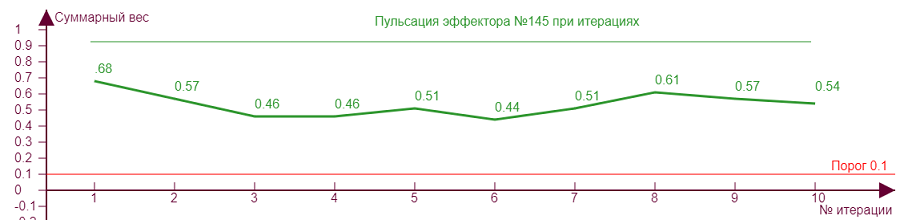	Вес рецепторов – 0,1 Порог – 0,1 Торможение – 0,3
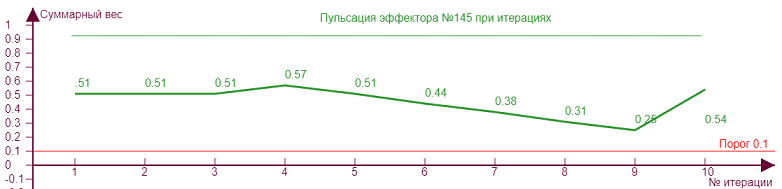	Вес рецепторов – 0,1 Порог – 0,1 Торможение – 0,6
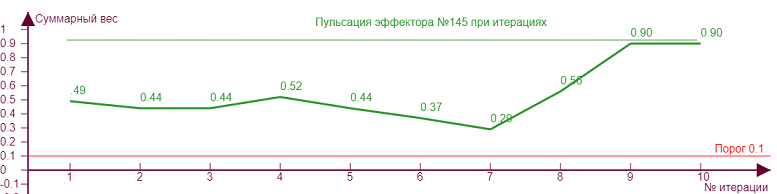	Вес рецепторов – 0,1 Порог – 0,1 Торможение – 0,7

В данном случае такие изломы находятся выше порога возбуждения и никак не сказываются на статусе эффектора, то есть несмотря на колебания веса он всегда находится в активном состоянии. Но возможны ситуации, когда тормозное влияние может не только выключить эффектор, но и сделать суммарный вес «отрицательным», что означает чрезмерную заторможенность эффектора. Такой эффект проявляется тем сильнее, чем больше ассиметричная нагрузка эффектора, то есть рецепторы в его охвате возбуждают его не равномерно.

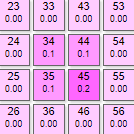		Эффектор №145 нагружен с сильным «перекосом» в сторону рецепторов 34,35,44, что приводит к соответствующему эффекторному рисунку. График роста его веса при итерациях уходит в отрицательную область значений. Порог – 0,1 Торможение – 0,1
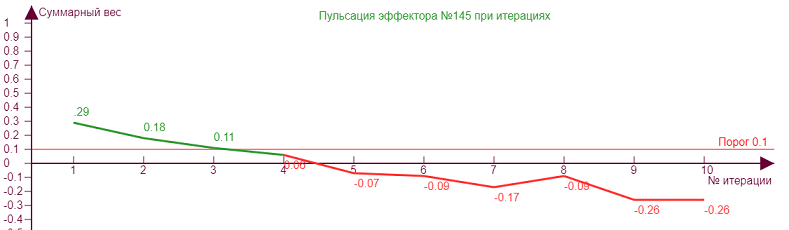			Порог – 0,1 Торможение – 0,4

Увеличим теперь порог до 0,3 и начнем наращивать уровень торможения. На графике появляется новый элемент – импульс пульсации. Это означает, что при таких значения параметров эффектор один раз «выключается», так как уровень возбуждения становится ниже либо равен порогу. Таких импульсов может быть несколько, и они могут возникать на разных этапах формирования итогового веса.

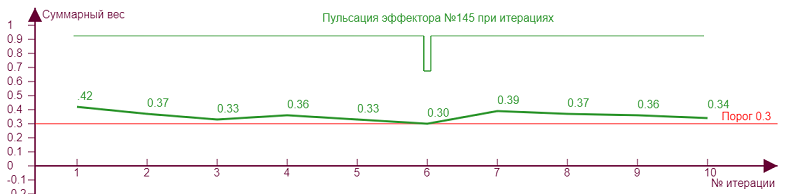	Порог – 0,1 Торможение – 0,4
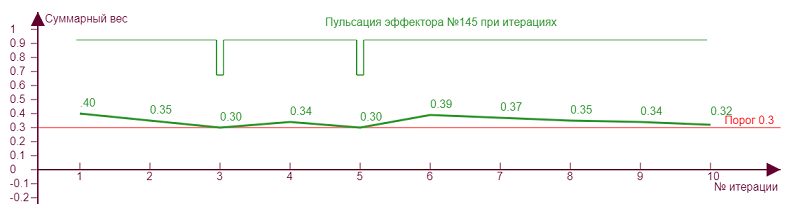	Порог – 0,3 Торможение – 0,31
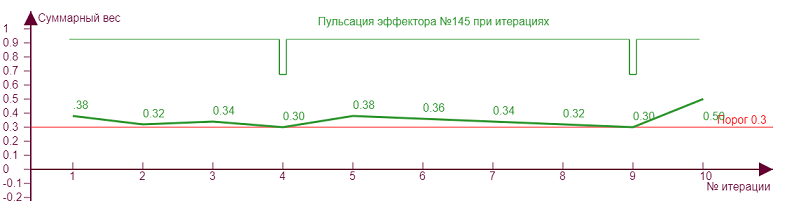	Порог – 0,3 Торможение – 0,36

Экспериментируя с разными значениями параметров можно заметить, что «пульсация» чаще при близких значениях порога и торможения для неравномерно загруженного эффектора, когда кривая веса и линия порога расположены близко, отчего и происходят их «касания», вызывающие пульсацию. При таких режимах нейросеть максимально неустойчива, и эффектор подобен маятнику, который получив импульс должен покачаться, чтобы успокоиться. Такие импульсы возможно оказывают влияние на итоговую разрядку нейрона, как бы модулируя его несущую частоту. А с учетом того, что неравномерность весов эффектора типична в реальной нейросети, так как при самообучении детектируемые примитивы практически всегда неоднородны, то можно предположить, что сам факт разрядки нейрона импульсами в какой то мере происходит как раз потому, что практически всегда возникают такие импульсы-щелчки при его активации.