Парадокс близнецов - обзор решений, гл.1

Парадокс близнецов – обзор решений

Путенихин П.В.

Оглавление, URL:

http://samlib.ru/p/putenihin_p_w/twin00.shtml

1. Классическое решение парадокса близнецов в СТО

Классическим решением парадокса близнецов называется решение, выполненное в рамках, в формализме теории, в которой он и был сформулирован, то есть, математическими средствами специальной теории относительности. Отметим, что специальную теорию относительности следует рассматривать в двух принципиально различных вариантах. Первый – это математическая теория, сформулированная в виде математической теоремы, исходными данными которой является второй постулат, который не требует доказательств. Именно так следует рассматривать математический инвариант скорости света. Теорема строго доказана и не имеет никаких внутренних логических противоречий, поэтому принципиально неопровержима. Второй вариант – это расширение математической теоремы на физическую реальность. И здесь неизбежны противоречия, поскольку инвариант реального физического параметра – скорости света теперь уже должен быть доказан в физическом эксперименте. И здесь возникает проблема, поскольку существует немало экспериментов, которые опровергают инвариантность скорости света [3, 8, 9].

По поводу парадокса близнецов в литературе и в интернете до сих пор идут многочисленные дискуссии. Предложено и продолжает предлагаться множество его решений (объяснений), из которых делаются выводы как о непогрешимости СТО, так и о её ложности. Впервые тезис, послуживший основой для формулировки парадокса, был изложен Эйнштейном в его основополагающей работе по специальной (частной) теории относительности "К электродинамике движущихся тел" в 1905 году:

"Если в точке A находятся двое синхронно идущих часов и мы перемещаем одни из них по замкнутой кривой с постоянной скоростью до тех пор, пока они не вернутся в A (...), то эти часы по прибытии в A будут отставать по сравнению с часами, остававшимися неподвижными...".

В дальнейшем этот тезис получил собственные имена "парадокс часов", "парадокс Ланжевена" и "парадокс близнецов". Последнее название прижилось, и в настоящее время чаще встречается формулировка не с часами, а с близнецами и космическими полётами: если один из близнецов улетает на космическом корабле к звёздам, то по возвращению он оказывается моложе своего остававшегося на Земле брата:

"Two twins A and B meet at an event P1, move away from each other, and then meet again at a later event P2. The twin A considers himself as at rest and predicts that B is younger than himself at P2 due to the relativistic time dilation. But according to the principle of relativity B can consider himself as at rest and A as travelling, and he then predicts that A is younger when they meet at P2. The twin paradox is these contradicting predictions" [1].

В нашем переводе это звучит так:

"Два близнеца A и B встречаются в событии P1, отходят друг от друга, а затем снова встречаются в более позднем событии P2. Близнец A считает себя находящимся в состоянии покоя и предсказывает, что B в P2 моложе себя из-за релятивистского замедления времени. Но согласно принципу относительности B может считать себя находящимся в состоянии покоя, а A – путешествующим, и затем он предсказывает, что A моложе, когда они встречаются в P2. Парадокс близнецов – это противоречивые предсказания".

И ещё одно описание сущности парадокса:

"Парадокс основан на неправильном применении понятия относительного движения и на игнорировании различия между инерциальными системами отсчета и неинерциальными. Состоит он в следующем.

Представим себе часы A, неподвижные в некоторой инерциальной системе отсчета. Пусть мимо них проходят с постоянной скоростью ν часы В, которые, пройдя известный путь, испытывают отрицательное ускорение, меняют знак скорости и вновь проходят со скоростью (‑ν) мимо часов В. В моменты прохождения часов A мимо часов В (туда и обратно) возможно непосредственное сравнение их показаний (без посредства световых сигналов). Такое сравнение должно обнаружить, что отстали часы В; по крайней мере, к такому выводу приводит применение формул для собственного времени, выведенных в § 14.

Но ведь движение относительно. Значит, можно считать неподвижными часы В. Другие же часы (А) будут, при таком рассмотрении, сперва равномерно удаляться, потом равномерно приближаться к часам B, и по тем же формулам § 14, как будто, должно оказаться, что теперь отстали часы A, в противоречии с полученным ранее результатом.

Разность показаний часов, находящихся в одной точке пространства, есть факт абсолютный и объективный (т. е. ни от системы отсчета, ни от способа рассмотрения не зависящий). Поэтому любой способ рассмотрения, если только он верен, должен приводить к одному и тому же результату. Противоречие в результате показывает, что где-то в рассуждениях допущена ошибка" [7, с.308].

Таким образом, парадокс, кажущееся противоречие в предсказаниях теории относительности возникает, если движущимся близнецом считать того, который оставался на Земле. В этом случае теперь уже улетавший в космос близнец должен ожидать, что остававшийся на Земле брат окажется моложе него. Так же и с часами: с точки зрения часов на экваторе движущимися следует считать часы на полюсе. Таким образом, и возникает противоречие: так кто же из близнецов окажется моложе? Какие из часов покажут время с отставанием?

Мы опираемся на определение понятия "парадокс" в логике как противоречия, полученного в результате логически формально правильного рассуждения, приводящего к взаимно противоречащим заключениям (Энциклопедический словарь), или как два противоположных утверждения, для каждого из которых имеются убедительные аргументы (Логический словарь). С этой позиции, "парадокс близнецов, часов, Ланжевена" парадоксом не является, поскольку даже довольно поверхностный анализ показывает отсутствие двух взаимоисключающих предсказаний теории.

Чаще всего парадоксу даётся простое объяснение: две рассматриваемые системы отсчёта на самом деле не являются равноправными. Близнец, который улетал в космос, в своём полёте не всегда находился в инерциальной системе отсчёта, в эти моменты он не может использовать уравнения Лоренца. Так же и с часами.

"Нетрудно видеть, что ошибка заключена в неучёте того, что часы A и часы B находились в этом воображаемом опыте в неодинаковых физических условиях: часы A никакому ускорению не подвергались и никаких толчков не испытывали, тогда как часы B подвергались ускорению и испытали толчок, изменивший знак их скорости. Другими словами, ошибка произошла из-за того, что обе системы отсчета (связанная с часами A и связанная с часами В) в приведенных рассуждениях предполагались равноправными, чего на самом деле нет: инерциальной является только система отсчета, связанная с часами А. Таково качественное разъяснение парадокса" [7, с.308].

Из этого следует сделать вывод: в СТО не может быть корректно сформулирован "парадокс часов", специальная теория не делает двух взаимоисключающих предсказаний. Считается, что полное решение задача получила после создания общей теории относительности, которая решила задачу точно и показала, что, действительно, в описанных случаях отстают движущиеся часы: часы улетавшего близнеца и часы на экваторе. "Парадокс близнецов" и часов, таким образом, можно считать рядовой задачей теории относительности.

Вместе с тем следует всё-таки осторожно подходить к "принадлежности" парадокса той или иной теории относительности:

"При изучении СТО указывается, что "парадокс близнецов" не может быть объяснен в рамках этой теории. … Этот парадокс не может быть разрешен в рамках СТО, так как рассматриваемые СО не равноправны (как это требуется в СТО): космический корабль не может рассматриваться ИСО, так как движется на отдельных участках траектории неравномерно. ... Только в рамках ОТО мы можем понять и объяснить "парадокс близнецов" естественным образом, опираясь на положения OТО" [6, c.297].

Следует обратить внимание на одно важное обстоятельство. На самом деле возвращение обратно и реальная встреча близнецов после полёта не обязательны, поскольку в неподвижной ИСО все часы синхронизированы и показывают одно и то же время. Если близнец-путешественник сравнит свои часы с часами в конечном пункте, это будет тождественно тому, что он сравнил свои часы с часами в пункте отлёта. Соответственно, это тождественно сравнению его возраста с возрастом брата, оставшегося на Земле. Иначе говоря, парадокс близнецов в рамках специальной теории относительности имеет строго корректную формулировку и допускает решение.

Отметим, что для уменьшения "этажности" уравнений, в частности, в преобразованиях Лоренца далее мы будем использовать световую систему единиц, в которой время измеряется в годах, расстояние – в световых годах, а скорость, соответственно, в световых годах за год. Сразу же замечаем, что скорость света в этой системе единиц измерения будет равна единице, а все скорости численно будут составлять некоторую долю от скорости света. В этом случае, например, одно из уравнений преобразований Лоренца примет следующий вид:

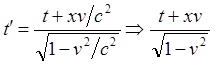
1.1 Корректные решения парадокса в СТО

Выше мы заявили, что парадокс близнецов в версии парадокса ровесников имеет корректное, непротиворечивое решение именно в специальной теории относительности, без обращения к формализму общей теории относительности. Покажем это, рассмотрев две системы отсчёта – ИСО AB и ИСО CD, рис.1.

Рис.1.1. Две ИСО, движущиеся относительно друг друга

Две ИСО изображены для наглядности в виде железнодорожных путей. Сразу же возникает вопрос, почему для каждой из них длина пути изображена разной? Суть в том, что любой путь, траектория имеет максимальную, исходную длину только в одной ИСО, собственной, в которой он неподвижен. За "хозяйку пути" мы произвольно выбрали ИСО AB. Это означает, что с точки зрения близнеца-землянина именно этот путь L_AB=AB пройдёт путешественник C со скоростью v.

Предположим, что в системах покоя двух ИСО их отрезки имеют одинаковую длину, то есть, AB = CD. Но для наблюдателя в ИСО AB "железнодорожный путь" CD является традиционным лоренцевым отрезком, который испытал при движении соответствующее сокращение до размеров CD. C его точки зрения длина этого отрезка пути CD равна:

   (1.1)

Здесь следует отметить, что при решении парадокса близнецов это обстоятельство, что с разных точек зрения отрезок имеет разную длину, весьма часто упускают из вида. С точки зрения ИСО AB время в пути наблюдателя C составит:

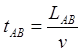   (1.2)

Поскольку с точки зрения ИСО AB время в ИСО CD замедленно, то в последней пройдёт меньшее время. Отметим, что это время таймерное, то есть это не абсолютные показания часов, а интервал времени между совпадением положений наблюдателя C с наблюдателями A и B:

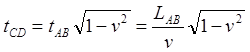   (1.3)

Понятно, что с точки зрения ИСО CD теперь уже путь AB испытал лоренцево сокращение, поэтому время в пути по его собственным часам также уменьшилось:

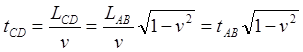
Как видим, с точки зрения наблюдателя в ИСО A он постарел на время t_AB, в то время как путешественник постарел только на время t_CD < t_AB. Но в данном случае оба близнеца сошлись во мнении относительно времени путешествия по часам путешественника. И тот и другой определили, что путешественник постарел на время t_CD. Разногласия возникнут у них при определении возраста близнеца, остававшегося на Земле. Когда путешественник прибывает в точку B, он сделает заключение, что в ИСО AB прошло иное время, нежели определил земной близнец. Действительно, как мы вычислили, по часам путешественника прошло время t_CD, следовательно, по его мнению, на Земле и на всех часах в ИСО A прошло меньшее время, поскольку все эти часы шли медленнее часов путешественника:

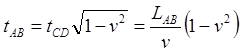
Но эти показания отличаются от показаний (1.2). Парадокс? Вовсе нет. Во-первых, прошедший интервал времени по любым часам не равен показаниям этих часов. Следовательно, во-вторых, при определении показаний часов нужно учитывать, что в момент начала удаления путешественника от Земли, показания часов B для него были не теми, что показания с точки зрения Земли. Если предположить, что моменту начала удаления часы путешественника и на Земле показывали время t₀, то в этот же момент с точки зрения путешественника часы B показывали время, согласно уравнению Лоренца:

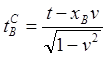   (1.4)

В соответствие с относительностью одновременности, любое событие в ИСО AB имеет разное время свершения с точки зрения разных наблюдателей в ИСО CD. В данном случае, наблюдатель в точке A "видит" показания часов B, равные t₀, а для наблюдателя C, находящегося на удалении x от этих часов, эти показания завышены, установлены в будущее (1.4).

Предварительно попробуем выяснить физический смысл этого довольно туманного слагаемого xv/c². Для этого обратимся к выкладкам, которые, собственно, и привели к выражению (1.4):

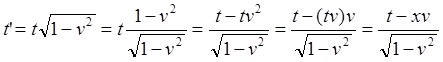   (1.5)

То есть, выражение (1.4) получено простыми алгебраическими преобразованиями, поэтому точно так же отражает эффект замедления времени в движущейся ИСО, в данном случае ИСО CD. В процессе преобразований мы выделили произведение tv, которое равно расстоянию, какое пройдёт движущаяся ИСО за это время. Таким образом, время t' – это время, которое будут показывать движущиеся часы, когда они удалятся на расстояние x. Иначе говоря, расстояние x соответствует положению этих часов, когда они показывают время t'. И наоборот, движущиеся часы покажут время t', когда они переместятся на расстоянии x.

Вполне обоснованно считаем, что это время нам известно, поскольку это реальные показания таймера в ИСО CD в момент прибытия наблюдателя C в точку B. Найдем по уравнению (1.5) соответствующие показания часов B с точки зрения этой движущейся ИСО:

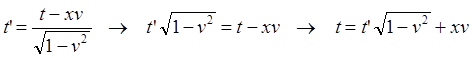
Выше мы определи физический смысл величины xv, в которой в нашем случае x=L_AB. Подставляем в полученное уравнение значения времени t' и величины xи находим время, прошедшее в ИСО AB с точки зрения наблюдателя C:

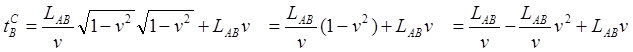
Из чего окончательно получаем:

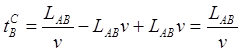   (1.6)

Итак, используя уравнение (1.5), мы нашли последнюю величину (1.6), ведущую к парадоксу близнецов – время в неподвижной ИСО AB с точки зрения путешественника. И эта величина показывает, что никакого парадокса нет.

Однако проведённые вычисления выглядят несколько прямолинейно, поскольку мы по существу использовали исходное уравнение (1.3), просто в обратном порядке. Понятно, что полученный результат полностью ему соответствует. Поэтому рассмотрим эту же картину в ином варианте.

В начальный момент отсчёта, когда путешественник начал удаляться от Земли, он, согласно уравнениям Лоренца, считает, что удалённые, встречные часы B в этот момент показывают время в будущем (1.4). Следовательно, с его точки зрения к моменту встречи с часами B они будут показывать время (1.4) плюс время в пути в ИСО AB с точки зрения ИСО CD с учетом замедления часов ИСО AB:

С точки зрения наблюдателя C в ИСО AB прошло время, интервал времени, равный времени в ИСО CD, испытавшему лоренцево замедление:

Однако прошедшее время, интервал времени отличается от показаний часов, поскольку показания равны исходному времени плюс прошедшее время, причём t = t₀ = 0:

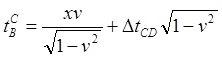
Преобразуем:

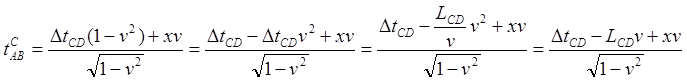
Мы рассматриваем ситуацию из ИСО C, поэтому

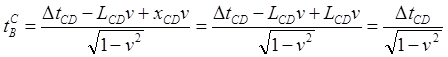
Уточним, что отрезом x_CD – это отрезок AB, каким он "видится" из ИСО CD. Далее с учетом уравнения (1.1) получаем

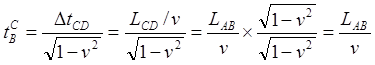 (1.7)

Таким образом, мы получили, что с точки зрения ИСО CD и путешественника C, часы B в ИСО AB показывают то же самое время (1.7), что и с точки зрения ИСО AB (1.2):

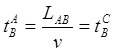
Возражение, что часы B – это другие часы, а не часы A, не имеет оснований, поскольку в неподвижной ИСО AB все часы тождественны, синхронны. Следовательно, часы B точно так же показывают возраст близнеца-землянина, как и часы A. Фактически мы рассматриваем тождественный парадокс ровесников и приходим к выводу, что собственно парадокса нет. Такой подход позволяет привести ещё одно, на наш взгляд, более простое решение задачи.

1.2 Парадокс ровесников

Как отмечено, в исходном варианте парадокса участники являются близнецами. Однако это определённо чрезмерное допущение, требующее обязательного возврата путешественника в исходную точку. С точки зрения СТО этот процесс считается невозможным, поскольку инерциальность движущейся ИСО на определённом этапе нарушается. Чрезмерность проявляется в том, что на самом деле показания всех часов в неподвижной ИСО одни и те же, поэтому возраст всех ровесников будет одним и тем же в любой точке этой ИСО. Это означает, что путешественнику не обязательно возвращаться обратно для того, чтобы сравнить свой возраст со своим близнецом. В конечной точке возраст ровесника равен возрасту близнеца в исходной точке, то есть, сравнение возраста путешественника-астронавта с возрастом ровесника тождественно его сравнению с возрастом оставшегося близнеца. Понятно, что под возрастом ровесником мы также можем подразумевать и просто показания часов, почему парадокс близнецов нередко отождествляют с парадоксом часов.

Итак, вновь обратимся к рис.1.1. Пусть традиционно возраст путешественника в конце пути с точки зрения неподвижной ИСО AB возрос на величину:

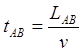
Тогда в подвижной ИСО CD пройдёт время:

Поскольку астронавт в конечной точке встретит ровесника своего остававшегося на Земле близнеца, то оба они придут к выводу: путешественник оказался моложе. Это соответствует картине с точки зрения неподвижной, земной ИСО AB. Но парадокс возникает, как считается, когда картину рассматривают с точки зрения подвижной ИСО CD, космолёта. Однако это мнение ошибочно. Действительно, в системе покоя этой подвижной ИСО CD длина пути AB видится укороченной вследствие релятивистского сокращения. И это известно наблюдателю C, что позволяет ему легко вычислить длину пути в системе покоя ИСО AB:

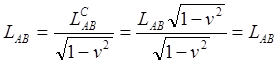
Здесь, как и ранее, верхний индекс C означает, что этот отрезок видится из ИСО CD. Из этого следует, что астронавту C также известно: с точки зрения ИСО AB он, астронавт переместится из начальной точки A в конечную точку B за время

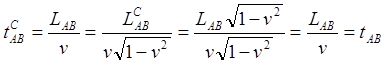
И вновь мы получили согласованное мнение наблюдателей в ИСО AB и ИСО CD: возраст астронавта в конце путешествия меньше возраста всех ровесников в неподвижной, земной системе отсчёта и, следовательно, меньше возраста оставшегося на Земле близнеца. Нет никакого противоречия, парадокса.

1.3 Мгновенный разворот

Однако и вариант с близнецами и возвратом путешественника обратно на Землю также допускает корректное решение в рамках специальной теории относительности. Нет принципиальных возражений против мгновенного разворота путешественника в дальней точке.

Действительно, казалось бы, налицо нарушение инерциальности, ведь разворот означает ускоренное движение, торможение. Но заметим, что с часами участников в этом случае ничего криминального не происходит.

Рассмотрим картину в точке разворота из неподвижной ИСО. Очевидно, что перед его началом показания часов участников равны:

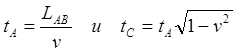
Если теперь путешественник мгновенно остановится, то показания часов t_A не изменятся, поскольку на них не оказывается никакого воздействия, в частности, нет никакого "падения" в гравитационном поле. И наблюдатель в ИСО AB и наблюдатель-астронавт в ИСО CD видят на часах B одно и то же время.

Но и показания часов C – путешественника также не должны измениться. Конечно, он испытывает огромное тормозящее, разворачивающее ускорение, которое создаёт эквивалентное гравитационное поле, подобное полю, например, Чёрной дыры. Следовательно, его часы испытают гравитационное красное смещение, а попросту замедлят своё движение вплоть до нуля. То есть за короткое время разворота показания часов и этого участника останутся теми же.

Согласно специальной теории относительности удалённые часы, часы в исходной точки, точке отлёта должны быть заново синхронизированы с часами астронавта, то есть, их показания должны быть "назначены" согласно уравнению (1.4). Но и это, в сущности, не является необходимым, поскольку значение имеют их показания не кажущиеся астронавту в точке разворота [4], а показания в момент возврата в эту исходную точку. А это прямо означает, что обратный путь будет полностью тождественен прямому пути, и показания таймеров участников на момент встречи просто удвоятся:

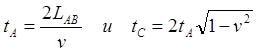
Таким образом, и в этом случае оба участника придут к согласованному мнению, что путешественник будет моложе, чем близнец, остававшийся на Земле.

1.4 Решение парадокса с учетом принципа относительности

Можно было бы сказать, что рассмотренные решения являются исчерпывающими и непротиворечивыми. С любой точки зрения путешественник-астронавт оказывается моложе своего близнеца-землянина, остававшегося неподвижным. Однако... Не случайно теория называется теорией относительности. И здесь мы обнаруживаем самое яркое проявление этой относительности: существует корректная точка зрения, согласно которой моложе оказывается остававшийся неподвижным близнец! Это, хотя и неожиданное и нигде ранее не рассмотренное обстоятельство, на самом деле оно является строго корректным результатом решения парадокса близнецов в специальной теории относительности.

Ещё раз обратимся к рис.1.1. Для простоты мы приняли, что длина космолёта CD в системе покоя ИСО CD в точности равна длине пути AB в системе покоя ИСО AB, и равны они L. Непосредственно это проявляется в том, что эти длины из смежных ИСО видны укороченными. То есть, с точки зрения условно неподвижной ИСО движущаяся относительно неё ИСО имеет, соответственно, длину:

Рассмотрим движение неподвижного наблюдателя B на Земле относительно космолёта. В некоторый момент времени с ним поравняется наблюдатель D в движущейся системе отсчёта космолёта, ИСО CD. В этот момент все участника запускают свои таймеры. С точки зрения ИСО AB длина космолёта видится укороченной:

Следовательно, по таймеру ИСО AB наблюдатель-землянин достигнет точки C за время:

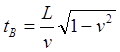
Но, с другой стороны, ему точно известна истинная длина этой ИСО – L, следовательно, по таймеру космолёта с его точки зрения пройдёт время:

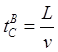
В свою очередь, и с точки зрения движущейся ИСО, космолёта пройдёт это же время, поскольку наблюдатель-землянин B преодолел её длину с той же скоростью:

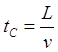
И, наконец, с точки зрения космолёта в ИСО AB пройдёт меньшее время вследствие лоренцева замедления:

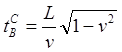
Как видим, оба наблюдателя, неподвижный на Земле B и путешественник-астронавт C пришли к согласованному мнению: t_C > t_B, моложе оказался землянин:

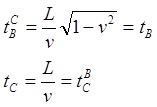
При всей его странности заметим, что это решение является странным лишь на первый, поверхностный взгляд. Увидеть его, это решение можно, например, в работе Ландау-Лившица:

"... для сравнения хода часов в двух системах отсчета необходимы несколько часов в одной системе и одни в другой. Поэтому этот процесс не симметричен по отношению к обеим системам. Всегда окажутся отстающими те часы, которые сравниваются с разными часами в другой системе отсчета" [2, т.2, с.23].

Действительно, в рассмотренных решениях мы сравнивали двое часов в одной ИСО с единственными часами в другой. И в обоих случаях получили отстающими эти единственные часы, возраст близнеца. Хотя следующее высказывание сделано по другому поводу (об неинерциальных системах), оно предельно точно описывает и рассмотренную ситуацию:

"... рассуждение, приводящее к результату, что покоящиеся часы должны оказаться отстающими, неправильно" [2, т.2, с.23].

Здесь под покоящимися часами мы понимаем условно покоящиеся, а не в традиционном понимании движения. Иначе говоря, покоящимся можно считать и космолёт, а не только Землю. Очевидно, такой результат будет как в случае ровесников, так и в случае близнецов с мгновенным разворотом космолёта в конечной точке движения.

1.5 Парадокс спешащих часов

В заключение отметим ещё один яркий эффект относительности, непосредственно связанный с двойственностью решения парадокса близнецов [5]. Наблюдатель в движущейся ИСО, например, в вагоне поезда смотрит в окно. Там он видит равномерно расставленные часы. Сравнивая их показания с собственными часами, он обнаружит, что показания часов снаружи всё время опережают показания его собственных часов. Как же так, часы снаружи спешат вопреки предсказаниям специальной теории относительности?

Но никакого противоречия нет. Каждые из промелькнувших за окном часов отстают по мере удаления. Но показания каждых новых часов по ходу движения всегда больше показаний предыдущих. Это и создаёт впечатление спешащих часов. На самом деле все часы в движущейся мимо ИСО отстают, а время в ней как таковое опережает время в условно неподвижной системе отсчёта наблюдателя.

Выводы

Корректные вычисления в парадоксе близнецов по правилам специальной теории относительности приводят к непротиворечивому результату. Точки зрения каждого из близнецов (ровесников) полностью совпадают: моложе оказывается тот из них, который рассматривается как реально движущийся относительно ИСО, за которой принудительно закреплена трасса, траектория движения.

Если закрепить трассу за другой ИСО, то результат будет противоположным, но по-прежнему моложе будет теперь уже другой участник, считающийся движущимся.

Литература

1.   Grøn Ø., Lecture Notes on the General Theory of Relativity, p.90. Springer (2009).

1. Ландау Л.Д. и Лифшиц Е.М., Теоретическая физика в десяти томах, т.II Теория поля. – М., «Наука», 1988
2. Маринов С. "Экспериментальные нарушения принципов относительности, эквивалентности и сохранения энергии", ФМР, 1995, №1, с.52-77, URL: http://www.macmep.ru/marinov.htm
3. Путенихин П.В., Преобразования Лоренца как иллюзия // Сборник статей XLI международной научной конференции "ТЕХНОКОНГРЕСС", ИД "Плутон", 8 апреля 2019, URL:
   https://t-nauka.ru/wp-content/uploads/k41.pdf с.45-51
4. Путенихин П.В., Три чуда СТО: парадокс спешащих часов // Научный электронный архив, URL: http://econf.rae.ru/article/9855 (дата обращения: 11.06.2019).
5. Розман Г.А. Теория относительности. – Псков: ПГПУ, 2005. – 256 с., URL: http://rozman2.narod.ru/oto.html
6. Фок В.А., Теория пространства, времени и тяготения. Изд. 2-е., доп. – М.: Гос. изд. физ.-мат. лит., 1961 г.
7. Штырков Е.И., Измерение параметров движения Земли и Солнечной системы // Вест. КРАУНЦ, Серия науки и Земле, 2005, №2. Вып. №6, c.135.
8. Эфирный ветер — сборник статей под ред. В.А.Ацюковского, URL:
   http://www.studfiles.ru/download.php?id=1667545&code=f6c93f7ccaa495b446e8cbb65dba2940